
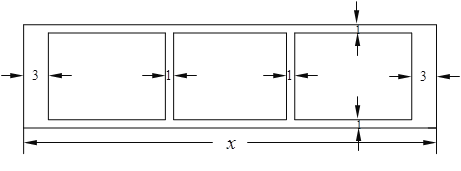
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知数据x1 , x2 , x3 , …,x100是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为x,平均数为y,方差为z,如果再加上马云2016年10月份的收入x101(约100亿元),则相对于x、y、z,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求证:{ ![]() }是等差数列;
}是等差数列;
(2)求an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 .
(注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …,xn的平均数)
为x1 , x2 , …,xn的平均数)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,D,E分别是BC,AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P﹣BC﹣A的平面角为γ,则α,β,γ的大小关系是( ) 
A.α<β<γ
B.α<γ<β
C.β<α<γ
D.γ<β<α
查看答案和解析>>
科目:高中数学 来源: 题型:
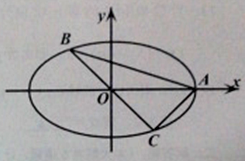
【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com