
分析 设A点的坐标为(x,y),∠ABC=α,∠ACB=2α,求出AB,AC的斜率,结合∠ACB=2∠ABC,得到斜率的关系,代入两直线的斜率整理得答案.
解答 解:设A点的坐标为(x,y),∠ABC=α,∠ACB=2α,
当$α=\frac{π}{4}$时,2α=$\frac{π}{2}$,此时A(2,±3);
当$α≠\frac{π}{4}$时,
则:${k}_{AB}=tanα=\frac{y}{x+1}$(x≠2)①,
${k}_{AC}=tan(180°-2α)=\frac{y}{x-2}$(x≠2),
即-tan2α=$-\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{y}{x-2}$ ②,
把①代人②,得$-\frac{2\frac{y}{x+1}}{1-(\frac{y}{x+1})^{2}}=\frac{y}{x-2}$,整理得3x2-y2=3,即${x}^{2}-\frac{{y}^{2}}{3}=1$(x≠2),
验证A(2,±3)适合上式.
又△ABC中,∠ABC<∠ACB,∴AB>AC,
∴顶点A的轨迹是双曲线的右半支,且不包含与x轴交点(1,0).
故顶点A的轨迹方程为${x}^{2}-\frac{{y}^{2}}{3}=1$,(x>1).
点评 本题考查轨迹方程的求法,解答此题的关键在于明确△ABC中,由∠ABC<∠ACB,可得AB>AC,得到顶点A的轨迹是双曲线的右半支,且不包含与x轴交点(1,0).是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -1 | C. | -5 | D. | -5或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(文)试卷(解析版) 题型:解答题
数列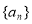 的前
的前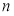 项和记为
项和记为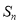 ,
, ,
,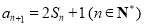 .
.
(Ⅰ)当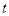 为何值时,数列
为何值时,数列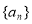 是等比数列;
是等比数列;
(Ⅱ)在(I)的条件下,若等差数列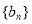 的前
的前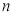 项和
项和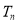 有最大值,且
有最大值,且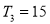 ,
,
又 ,
,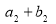 ,
, 成等比数列,求
成等比数列,求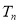 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com