
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() 是2与
是2与![]() 的等差中项.
的等差中项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若用![]() 代换曲线
代换曲线![]() 的普通方程中的
的普通方程中的![]() 得到曲线
得到曲线![]() 的方程,若
的方程,若![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)设数列{bn}的前n项和为Tn,且Tn+![]() =λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
=λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 的参数方程是
的参数方程是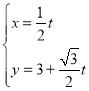 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),则b的取值范围为( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com