
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在其定义域内是单调函数,求实数
在其定义域内是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的最大值是2,求实数
的最大值是2,求实数![]() 的值;
的值;
(3)求函数![]() 的最小值.
的最小值.
【答案】(1)![]() 或
或![]() ;(2)3或
;(2)3或![]() ;(3)当
;(3)当![]() 时,最小值
时,最小值![]() ;当
;当![]() 时,最小值
时,最小值![]()
【解析】
![]() 的图象开口向下,对称轴
的图象开口向下,对称轴![]() ,
,
(1)若函数![]() 在其定义域
在其定义域![]() 内是单调函数,根据对称轴不在已知区间内,列出不等式解出即可;
内是单调函数,根据对称轴不在已知区间内,列出不等式解出即可;
(2)分类讨论,考虑对称轴![]() 与已知区间的三种情况进行讨论,根据单调性求出最值的表达式,解出
与已知区间的三种情况进行讨论,根据单调性求出最值的表达式,解出![]() 即可;
即可;
(3)结合端点0,1与对称轴的远近及开口方向进行求解.
![]() 的图象开口向下,对称轴
的图象开口向下,对称轴![]()
(1)若函数![]() 在其定义域
在其定义域![]() 内是单调函数,
内是单调函数,
![]() 或
或![]() ;
;
(2)①当![]() 时,函数
时,函数![]() 在其定义域
在其定义域![]() 内是单调递增,
内是单调递增,
当![]() 时函数有最大值
时函数有最大值![]()
![]() ;
;
②![]() 时,函数
时,函数![]() 在其定义域
在其定义域![]() 内是单调递减
内是单调递减
当![]() 时函数有最大值
时函数有最大值![]()
![]() ,
,
③![]() 时,函数
时,函数![]() 在其定义域
在其定义域![]() 内先增后减,
内先增后减,
当![]() 时函数有最大值
时函数有最大值![]() ,
,
解可得,![]() 或
或![]() ,经检验均不符合题意,
,经检验均不符合题意,
综合可得![]() 的值为3或
的值为3或![]() .
.
(3)①若![]() 即
即![]() 时,
时,![]() 时,函数取得最小值
时,函数取得最小值![]() ,
,
②若![]() 即
即![]() 时,
时,![]() 时,函数取得最小值
时,函数取得最小值![]() .
.
即当![]() 时,最小值
时,最小值![]() ;当
;当![]() 时,最小值
时,最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?( )(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)
A.1B.3C.5D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
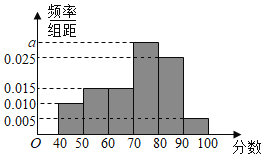
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | 0.10 |
三组 | 10≤t<15 | 10 | ② |
四组 | 15≤t<20 | ① | 0.50 |
五组 | 20≤t≤25 | 30 | 0.30 |
合计 | 100 | 1.00 |

解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的左顶点
的左顶点![]() 为圆心作圆
为圆心作圆![]() :
:![]() ,设圆
,设圆![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与点
与点![]() .
.
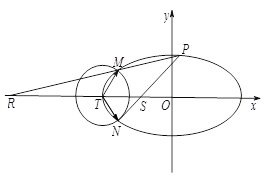
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,且直线
的任意一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 为坐标原点,
为坐标原点,
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸![]() 边形
边形![]() 玫瑰园的
玫瑰园的![]() 个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
(1)求出玫瑰园里玫瑰总棵树![]() 的表达式.
的表达式.
(2)花园里能否恰有99棵玫瑰?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个圆周上有9个点,以这9个点为顶点作3个三角形.当这3个三角形无公共顶点且边互不相交时,我们把它称为一种构图.满足这样条件的构图共有( )种.
A. 3 B. 6 C. 9 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com