
分析 (1)由题意可得-1,1为f(x+2)=0的解,可得m=1,即为$\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$=1,可得a+2b+3c=(a+2b+3c)($\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$),再由三元均值不等式即可得证;
(2)由$\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$=1,两边平方,结合二元均值不等式和累加法,即可得证.
解答 证明:(1)f(x+2)≥0即为m-|x|≥0的解集为[-1,1],
可得-1,1为f(x+2)=0的解,可得m=1,
即为$\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$=1,a,b,c>0,
则a+2b+3c=(a+2b+3c)($\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$)
≥3$\root{3}{6abc}$•3$\root{3}{\frac{1}{6abc}}$=9,
当且仅当a=2b=3c取得等号;
(2)由$\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$=1,可得
($\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$)2=1,
即有$\frac{1}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$+$\frac{1}{9{c}^{2}}$+$\frac{1}{ab}$+$\frac{2}{3ac}$+$\frac{1}{3bc}$=1,
而$\frac{1}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$≥$\frac{1}{ab}$,$\frac{1}{4{b}^{2}}$+$\frac{1}{9{c}^{2}}$≥$\frac{1}{3bc}$,
$\frac{1}{{a}^{2}}$+$\frac{1}{9{c}^{2}}$≥$\frac{2}{3ac}$,
累加可得$\frac{1}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$+$\frac{1}{9{c}^{2}}$≥$\frac{1}{2ab}$+$\frac{1}{6bc}$+$\frac{1}{3ac}$,
即有1-($\frac{1}{ab}$+$\frac{2}{3ac}$+$\frac{1}{3bc}$)≥$\frac{1}{2ab}$+$\frac{1}{6bc}$+$\frac{1}{3ac}$,
则$\frac{3}{2ab}$+$\frac{1}{2bc}$+$\frac{1}{ac}$≤1,
即为$\frac{1}{ab}$+$\frac{2}{3ac}$+$\frac{1}{3bc}$≤$\frac{2}{3}$成立.
点评 本题考查不等式的证明,注意运用均值不等式和不等式的性质和累加法,同时考查绝对值表达式的解法,考查化简整理的运算能力,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 圆 | C. | 双曲线 | D. | 椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 综合得分k的取值范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
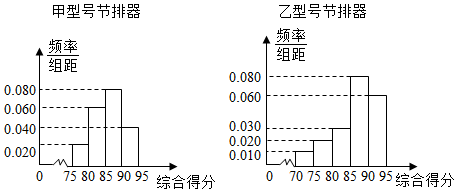
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com