Question

【题目】设函数f(x)＝ax2－1－lnx，其中a∈R．

（1）若a＝0，求过点(0，－1)且与曲线y＝f(x)相切的直线方程；

（2）若函数f(x)有两个零点x1，x2，

① 求a的取值范围；

② 求证：f ′(x1)＋f ′(x2)＜0．

Answer 1

【答案】(1) y＝－x－1 (2) ① (0，e)．②见解析

【解析】试题分析：（1）设切点为T(x0，－1－lnx0)，得切线：y＋1＋lnx0＝－ ( x－x0)，将点(0，－1)代入求解即可；

（2）①求导f ′(x)＝，讨论a≤0，和a＞0时函数的单调性求解即可；

②由x1，x2是函数f(x)的两个零点(不妨设x1＜x2)，得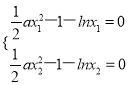 ，两式作差得a(x1＋x2)＝，代入要证得式子得2ln＋－＞0，令h(x)＝2lnx＋－x，x∈(0，1)，求导利用单调性求最值即可证得.

试题解析：

（1）当a＝0时，f(x)＝－1－lnx，f ′(x)＝－．

设切点为T(x0，－1－lnx0)，

则切线方程为：y＋1＋lnx0＝－ ( x－x0)．

因为切线过点(0，－1)，所以 －1＋1＋ln x0＝－(0－x0)，解得x0＝e．

所以所求切线方程为y＝－x－1．

（2）① f ′(x)＝ax－＝，x＞0．

(i) 若a≤0，则f ′(x)＜0，所以函数f(x)在(0，＋∞)上单调递减，

从而函数f(x)在(0，＋∞)上至多有1个零点，不合题意．

(ii)若a＞0，由f ′(x)＝0，解得x＝．

当0＜x＜时， f ′(x)＜0，函数f(x)单调递减；当x＞时， f ′(x)＞0，f(x)单调递增，

所以f(x)min＝f()＝－ln－1＝－－ln．

要使函数f(x)有两个零点，首先 －－ln＜0，解得0＜a＜e．

当0＜a＜e时，＞＞．

因为f()＝＞0，故f()·f()＜0．

又函数f(x)在(0，)上单调递减，且其图像在(0，)上不间断，

所以函数f(x)在区间(0，)内恰有1个零点．

考察函数g(x)＝x－1－lnx，则g′(x)＝1－＝．

当x∈(0，1)时，g′(x)＜0，函数g(x)在(0，1)上单调递减；

当x∈(1，＋∞)时，g′(x)＞0，函数g(x)在(1，＋∞)上单调递增，

所以g(x)≥g(1)＝0，故f()＝－1－ln≥0．

因为－＝＞0，故＞．

因为f()·f()≤0，且f(x)在(，＋∞)上单调递增，其图像在(，＋∞)上不间断，

所以函数f(x)在区间(，] 上恰有1个零点，即在(，＋∞)上恰有1个零点．

综上所述，a的取值范围是(0，e)．

②由x1，x2是函数f(x)的两个零点(不妨设x1＜x2)，得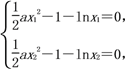

两式相减，得 a(x12－x22)－ln＝0，即a(x1＋x2) (x1－x2)－ln＝0，

所以a(x1＋x2)＝．

f ′(x1)＋f ′(x2)＜0等价于ax1－＋ax2－＜0，即a(x1＋x2)－－＜0，

即－－＜0，即2ln＋－＞0．

设h(x)＝2lnx＋－x，x∈(0，1)．则h′(x)＝－－1＝＝－＜0，

所以函数h(x)在(0，1)单调递减，所以h(x)＞h(1)＝0．

因为∈(0，1)，所以2ln＋－＞0，

即f ′(x1)＋f ′(x2)＜0成立．