
【题目】已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
【答案】(1)a1=1(2)an=2n-1,n∈N*.(3)k=2,t=3.
【解析】试题分析:(1)由![]() ,得
,得![]() ,解方程即可得结果;(2)因为
,解方程即可得结果;(2)因为![]() ,两式相减可得
,两式相减可得![]() 再得
再得![]() ,再相减可得
,再相减可得![]() 是等差数列,从而可得结果;(3)由(2)可知
是等差数列,从而可得结果;(3)由(2)可知![]() ,根据
,根据![]() 成等比数列可得
成等比数列可得![]() ,只需证明以上等式无整数解即可.
,只需证明以上等式无整数解即可.
试题解析:解:(1)由3T1=S12+2S1,得3a12=a12+2a1,即a12-a1=0.
因为a1>0,所以a1=1.
(2)因为3Tn=Sn2+2Sn, ①
所以3Tn+1=Sn+12+2Sn+1,②
②-①,得3an+12=Sn+12-Sn2+2an+1.
因为an+1>0,
所以3an+1=Sn+1+Sn+2, ③
所以3an+2=Sn+2+Sn+1+2,④
④-③,得3an+2-3an+1=an+2+an+1,即an+2=2an+1,
所以当n≥2时, ![]() =2.
=2.
又由3T2=S22+2S2,得3(1+a22)=(1+a2)2+2(1+a2),
即a22-2a2=0.
因为a2>0,所以a2=2,所以![]() =2,所以对n∈N*,都有
=2,所以对n∈N*,都有![]() =2成立,
=2成立,
所以数列{an}的通项公式为an=2n-1,n∈N*.
(3)由(2)可知Sn=2n-1.
因为S1,Sk-S1,St-Sk成等比数列,
所以(Sk-S1)2=S1(St-Sk),即(2k-2)2=2t-2k,
所以2t=(2k
由于Sk-S1≠0,所以k≠1,即k≥2.
当k=2时,2t=8,得t=3.
当k≥3时,由(*),得(2k-1)2-32k-2+1为奇数,
所以t-2=0,即t=2,代入(*)得22k-2-32k-2=0,即2k=3,此时k无正整数解.
综上,k=2,t=3.


科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,下列数值排序正确的是( ) 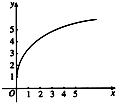
A.0<f′(2)<f′(3)<f(3)﹣f(2)
B.0<f′(3)<f(3)﹣f(2)<f′(2)
C.0<f(3)<f′(2)<f(3)﹣f(2)
D.0<f(3)﹣f(2)<f′(2)<f′(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率
的离心率 ![]() ,过点A(0,﹣b)和B(a,0)的直线与原点的距离为
,过点A(0,﹣b)和B(a,0)的直线与原点的距离为 ![]() .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点,问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题:若O是线段AB上一点,则有| ![]() |
| ![]() +|
+| ![]() |
| ![]() =
= ![]() .将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC
.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC ![]() +S△OCA
+S△OCA ![]() +S△OBA
+S△OBA ![]() =
= ![]() ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有 .
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用寒假进行社会实践活动,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是
人进行了一次生活习惯是
否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得
到如下统计表和各年龄段人数频率分布直方图:
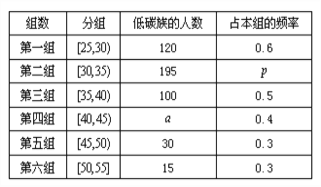
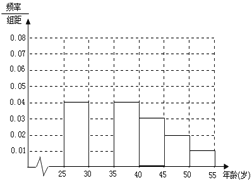
(I)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(II)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取![]() 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取![]() 人作为领队,求选取的
人作为领队,求选取的![]() 名领队中恰有1人年龄在
名领队中恰有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=8y.AB是抛物线C的动弦,且AB过F(0,2),分别以A,B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com