
【题目】对于命题:若O是线段AB上一点,则有| ![]() |
| ![]() +|
+| ![]() |
| ![]() =
= ![]() .将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC
.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC ![]() +S△OCA
+S△OCA ![]() +S△OBA
+S△OBA ![]() =
= ![]() ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有 .
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有 .
【答案】若O为四面体ABCD内一点,则有VO﹣BCD? ![]() +VO﹣ACD?
+VO﹣ACD? ![]() +VO﹣ABD?
+VO﹣ABD? ![]() +VO﹣ABC?
+VO﹣ABC? ![]() =
= ![]()
【解析】解:由平面图形的性质类比猜想空间几何体的性质,
一般的思路是:点到线,线到面,或是二维变三维,面积变体积;
由题目中点O在三角形ABC内,则有结论S△OBC ![]() +S△OCA
+S△OCA ![]() +S△OBA
+S△OBA ![]() =
= ![]() ,
,
我们可以推断若O为四面体ABCD内一点,则有VO﹣BCD ![]() +VO﹣ACD
+VO﹣ACD ![]() +VO﹣ABD
+VO﹣ABD ![]() +VO﹣ABC
+VO﹣ABC ![]() =
= ![]() .
.
所以答案是:若O为四面体ABCD内一点,则有VO﹣BCD ![]() +VO﹣ACD
+VO﹣ACD ![]() +VO﹣ABD
+VO﹣ABD ![]() +VO﹣ABC
+VO﹣ABC ![]() =
= ![]() .
.
【考点精析】利用类比推理对题目进行判断即可得到答案,需要熟知根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ) 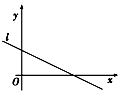
A.已知购买一张彩票中奖的概率为 ![]() ,则购买1000张这种彩票一定能中奖
,则购买1000张这种彩票一定能中奖
B.互斥事件一定是对立事件
C.如图,直线l是变量x和y的线性回归方程,则变量x和y相关系数在﹣1到0之间
D.若样本x1 , x2 , …xn的方差是4,则x1﹣1,x2﹣1,…xn﹣1的方差是3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现要在边长为100m的正方形ABCD内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为xm(x不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为 ![]() m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m.
m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m. 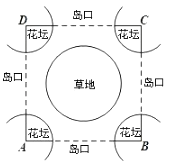
(1)求x的取值范围;(运算中 ![]() 取1.4)
取1.4)
(2)若中间草地的造价为a元/m2 , 四个花坛的造价为 ![]() 元/m2 , 其余区域的造价为
元/m2 , 其余区域的造价为 ![]() 元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
(1)求证:直线l恒过定点;
(2)当m变化时,求点P(3,1)到直线l的距离的最大值;
(3)若直线l分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点. 
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)是否存在实数![]() ,对任意的
,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立,若存在求出
恒成立,若存在求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com