练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，点P是边长为1的正六边形ABCDEF的边上的一个动点，设 =x +y ，则x+y的最大值为 ．

    【答案】2
    【解析】解：六边形边长为1，把向量 和向量 ，沿着AD方向和垂直于AD两个方向分解． 设AD方向为x轴，垂直于AD方向为y轴如图：
    那么 = =（﹣ ， ），
    =（﹣ ，﹣1﹣ ），
    =（﹣ x﹣ y， x﹣（1+ ）y），
    所以，当 的横坐标最小的时候，x+y最大．
    那么，当P与D重合时，满足这一条件．
    此时AP=2，x+y=2；最大值为2；
    故答案为：2．

    设六边形边长为1，把向量 ，和向量 ，沿着AD方向和垂直于AD两个方向分解．设AD方向为x轴，垂直于AD方向为y轴距离坐标系，得到 的坐标，分析x+y取最大值时P的位置．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某工厂为了对新研发的一种产品进行合理定价，随机抽取了6个试销售数据，得到第i个销售单价xi（单位：元）与销售yi（单位：件）的数据资料，算得
    （1）求回归直线方程 ；
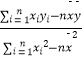    （2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入﹣成本） 附：回归直线方程 中， = ， = ﹣ ，其中 ， 是样本平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 通项公式为 ．
    （1）计算f（1），f（2），f（3）的值；
    （2）比较f（n）与1的大小，并用数学归纳法证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1： （a＞b＞0）的离心率为 ，且过点（1， ）．
    （1）求C1的方程；
    （2）设直线l同时与椭圆C1和抛物线C2：y2=4x相切，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为t1小时，其余工人加工完乙型装置所需时间为t2小时．

    设f(x)＝t1＋t2．

    （Ⅰ）求f(x)的解析式，并写出其定义域；

    （Ⅱ）当x等于多少时，f(x)取得最小值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于命题：若O是线段AB上一点，则有| | +| | = ．将它类比到平面的情形是：若O是△ABC内一点，则有S△OBC +S△OCA +S△OBA = ，将它类比到空间情形应该是：若O是四面体ABCD内一点，则有 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱ABC－A1B1C1中，AB＝AC，E是BC的中点，求证：

    （Ⅰ）平面AB1E⊥平面B1BCC1；

    （Ⅱ）A1C//平面AB1E．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）对任意的x∈（﹣ ， ）满足f′（x）cosx+f（x）sinx＞0（其中f′（x）是函数f（x）的导函数），则下列不等式成立的是（ ）
    A. f（﹣ ）＜f（﹣ ）
    B. f（ ）＜f（ ）??
    C.f（0）＞2f（ ）
    D.f（0）＞ f（ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的左、右焦点为F1、F2 ， 离心率为e．直线l：y=ex+a与x轴、y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设 =λ ．
    （1）证明：λ=1﹣e2；
    （2）若λ= ，△MF1F2的周长为6；写出椭圆C的方程；
    （3）确定λ的值，使得△PF1F2是等腰三角形．

    查看答案和解析>>

    同步练习册答案