练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．将两对双胞胎姐妹与另一对非双胞胎姐妹共六位同学排成一行，则双胞胎姐妹间各自不相邻的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{7}{15}$C．$\frac{1}{2}$D．$\frac{3}{5}$

    分析 将两对双胞胎姐妹与另一对非双胞胎姐妹共六位同学排成一行，先求出基本事件总数，再求出双胞胎姐妹间各自不相邻包含的基本事件个数，由此能求出双胞胎姐妹间各自不相邻的概率．

    解答 解：将两对双胞胎姐妹与另一对非双胞胎姐妹共六位同学排成一行，
    基本事件总数n=${A}_{6}^{6}$=720，
    双胞胎姐妹间各自不相邻包含的基本事件个数m=${A}_{6}^{6}-{A}_{2}^{2}{A}_{2}^{2}{A}_{4}^{4}$-${A}_{2}^{2}{A}_{3}^{3}{A}_{4}^{2}$-${A}_{2}^{2}{A}_{3}^{3}{A}_{4}^{2}$=336，
    ∴双胞胎姐妹间各自不相邻的概率为p=$\frac{m}{n}=\frac{7}{15}$．
    故选：B．

    点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．设动直线l：y=kx+m（其中k，m为整数）与椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$交于不同两点A，B，与双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$交于不同两点C，D，且$\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{0}$，则符合上述条件的直线l共有（　　）
    A．5条B．7条C．9条D．11条

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设A，B，C，D是平面上互异的四个点，若（$\overrightarrow{DB}$+$\overrightarrow{DC}$-2$\overrightarrow{DA}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）=0，则△ABC的形状是（　　）
    A．直角三角形B．等腰三角形C．锐角三角形D．钝角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

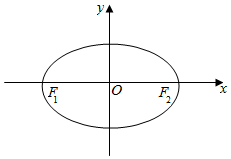    7．已知F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0）为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点P在椭圆C上，且△PF1F2面积的最大值为$\sqrt{3}$．
    （Ⅰ）求椭圆C的方程
    （Ⅱ）若直线l与椭圆C交于A，B两点．△OAB的面积为1，$\overrightarrow{OG}$=s$\overrightarrow{OA}$+t$\overrightarrow{OB}$（s，t∈R），当点G在椭圆C上运动时，试问s2+t2是否为定值，若是定值，求出这个定值，若不是定值，求出s2+t2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．过点P（1，-1）作圆x2+y2-2x-2y+1=0的切线，求切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．甲、乙、丙人应邀参加某综艺栏目的猜数游戏，猜中则游戏结束，主持人先给出数字所在区间[3，10]，让甲猜（所猜数字为整数，下同），如果甲猜中，甲将获得1000元奖金；如果甲未猜中，主持人给出数字所在区间[5，8]，让乙猜，如果乙猜中，甲和乙均可获得5000元奖金；如果乙未猜中，主持人给出数字所在区间[6，7]，让丙猜，如果丙猜中，甲、乙和丙均可获得2000元奖金，否则游戏结束．
    （1）求甲至少获得5000元奖金的概率；
    （2）记乙获得的奖金为X元，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．2015年12月27日全国人大常委会表决通过了人口与计划生育法修正案全面二孩定于20I6年1月1日起正式实施，为了解适龄民众对放开生育二胎政策的态度，某机构从某市选取70后和80后作为调查对象．随机调查了100位，得到数据如下表：
     生二孩不生二孩合计
    70后301545
    80后451055
    合计7525100
    （1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若以该市70后公民中随机抽取3位，记其中生二孩的人数为X，求随机变量X的分布列和数学期望．
    （2）根据调查数据，是否在犯错误的概率不超过0.1的前提下（有90%以上自把握）认为“生二孩与年龄有关”？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知x1，x2是关于x的一元二次方程4kx2-4kx+k+1=0的两个实数根．
    （1）求实数k，使（2x1-x2）（x1-2x2）=-$\frac{3}{2}$；
    （2）求使$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$-2的值为整数的实数k的整数值；
    （3）若k=-2，λ=$\frac{{x}_{1}}{{x}_{2}}$，试求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．圆周上有20个点，过任意两点可画一条弦，这些弦在圆内的交点最多能有4845个．

    查看答案和解析>>

    同步练习册答案