
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 经过点
经过点![]() .设椭圆
.设椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,右准线与
,右准线与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
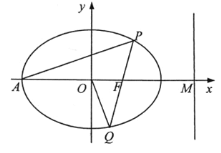
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() (
(![]() 在
在![]() 轴上方),直线
轴上方),直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且直线
,且直线![]() 与
与![]() 垂直,求直线
垂直,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据题意先得![]() ,
,![]() ,
,![]() ,由
,由![]() 为
为![]() 的中点,椭圆过点
的中点,椭圆过点![]() ,列出关系式,求出
,列出关系式,求出![]() ,
,![]() ,即可得出椭圆方程;
,即可得出椭圆方程;
(2)先由题意确定直线![]() 的斜率必存在且大于0,设直线
的斜率必存在且大于0,设直线![]() 的方程为:
的方程为:![]() ,联立直线与椭圆方程,结合韦达定理与题中条件,即可求出结果.
,联立直线与椭圆方程,结合韦达定理与题中条件,即可求出结果.
(1)因为![]() ,
,![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,
的中点,
所以![]() ,则
,则![]() .
.
即![]() ,所以
,所以![]() ,
,![]() .
.
因为点![]() 在椭圆上,
在椭圆上,
所以 ,
,
又因为![]() ,所以
,所以![]() ,则
,则![]() ,
,![]() .
.
所以椭圆的标准方程为![]() .
.
(2)由题意直线![]() 的斜率必存在且大于0,
的斜率必存在且大于0,
设直线![]() 的方程为:
的方程为:![]() .
.
代入椭圆方程并化简得:![]() ,
,
因为![]() ,
,
得![]() ,
, ,
,
当![]() 时,
时,![]() 的斜率不存在,此时
的斜率不存在,此时![]() 不符合题意.
不符合题意.
当![]() 时,直线
时,直线![]() 的方程为:
的方程为:![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的方程为:
的方程为:![]() ,
,
两直线联立解得:![]() ,因为
,因为![]() 在椭圆上,
在椭圆上,
所以![]() ,化简得:
,化简得:![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
此时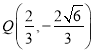 .
.
直线![]() 的斜率为
的斜率为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系中,以原点为极点,以![]() 轴非负半轴为极轴建立极坐标系, 已知曲线
轴非负半轴为极轴建立极坐标系, 已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 和
和![]() ,圆
,圆![]() 是以
是以![]() 为圆心,半径为
为圆心,半径为![]() 的圆,点
的圆,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 所在的直线交于点
所在的直线交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)已知![]() ,
,![]() 是曲线
是曲线![]() 上的两点,若曲线
上的两点,若曲线![]() 上存在点
上存在点![]() ,满足
,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若直线l:x+y=0与圆C交于A,B两点,求弦AB的长;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,四个点
中,四个点 ,
, ,
,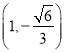 ,
,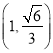 中有3个点在椭圆
中有3个点在椭圆![]() :
:![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明:存在常数
,证明:存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
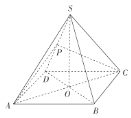
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动的真谛不仅在于竞技,更在于增强人民体质,培养人们爱国主义、集体主义、顽强拼搏的精神.足球是人类交流的另类“语言”,而其他竞技方式,无论从深度到广度,从速度到力度,都难以与足球比肩,就交流与表达而言,足球是人类最能展露自己天性的运动.
(1)已知某国每年注册足球运动员的人数![]() (万人)与该国年度国际足联排名
(万人)与该国年度国际足联排名![]() 线性相关,统计数据如下表:
线性相关,统计数据如下表:

求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测该国年度国际足联排名为第
,并预测该国年度国际足联排名为第![]() 时注册足球运动员的人数;(参考公式:
时注册足球运动员的人数;(参考公式: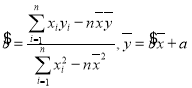 )
)
(参考数据:![]() ;
;![]() )
)
(2)从该国中学生中选出![]() 名男生进行颠球挑战,若能一次性连续颠球超过
名男生进行颠球挑战,若能一次性连续颠球超过![]() 个就可获得一个奖励足球,每人只能挑战一次.已知这
个就可获得一个奖励足球,每人只能挑战一次.已知这![]() 名男生每人能够一次性连续颠球超过
名男生每人能够一次性连续颠球超过![]() 个的概率均为
个的概率均为![]() ,且相互独立.求这
,且相互独立.求这![]() 名男生获得奖励足球个数
名男生获得奖励足球个数![]() 的数学期望
的数学期望![]() 及获得奖励足球超过
及获得奖励足球超过![]() 个的概率(精确到
个的概率(精确到![]() ).(参考数据:
).(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线
,直线![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的上方).
轴的上方).
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com