
已知命题p:函数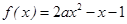 (a≠0)在(0,1)内恰有一个零点;命题q:函数
(a≠0)在(0,1)内恰有一个零点;命题q:函数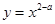 在(0,+
在(0,+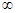 )上是减函数.若p且
)上是减函数.若p且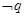 为真命题,则实数a的取值范围是( )
为真命题,则实数a的取值范围是( )
| A.a>1 | B.a≤2 | C.1<a≤2 | D.a≤l或a>2 |
C
解析试题分析:a=0时,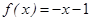 有零点-1,不符合题意;
有零点-1,不符合题意;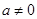 时,函数
时,函数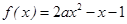 (a≠0)在(0,1)内恰有一个零点,由于f(0)=-1<0,根据二次函数的图像,共有两种情况:
(a≠0)在(0,1)内恰有一个零点,由于f(0)=-1<0,根据二次函数的图像,共有两种情况:
1.f(x)在(0,1)上是单调函数,则f(0)·f(1)<0
所以 -1(2a-2)<0,解得a>1;
2.f(x)的顶点在(0,1)之间,且开口向下即a<0,f(x)=0有相等实根,所以△=0,即1+8a=0,解得=- ,此时x=-2与题意不符,舍去;综合可知,a>1,即p: a>1.
,此时x=-2与题意不符,舍去;综合可知,a>1,即p: a>1.
因为,函数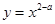 在(0,+
在(0,+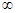 )上是减函数,所以2-a<0,a>2,
)上是减函数,所以2-a<0,a>2, 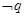 :
: 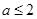 .
.
由p且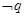 为真命题,知,p: a>1且
为真命题,知,p: a>1且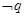 :
: 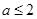 ,故1<a≤2,选C。
,故1<a≤2,选C。
考点:本题主要考查幂函数的性质,二次函数的零点,复合命题的概念。
点评:中档题,涉及命题的题目,往往综合性较强,需要综合应用数学知识的解题。


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:单选题
命题“若△ABC不是等腰三角形,则它的任何两个内角不相等.”的逆否命题是( )
| A.“若△ABC是等腰三角形,则它的任何两个内角相等” |
| B.“若△ABC任何两个内角不相等,则它不是等腰三角形” |
| C.“若△ABC有两个内角相等,则它是等腰三角形” |
| D.“若△ABC任何两个角相等,则它是等腰三角形” |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若向量a=(x,3)(x∈R),则“x=4”是“|a|=5”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列命题中错误的是
A.命题“若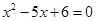 ,则 ,则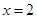 ”的逆否命题是“若 ”的逆否命题是“若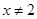 ,则 ,则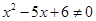 ” ” |
B.对命题 : : ,使得 ,使得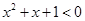 ,则 ,则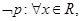 则 则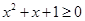 |
C.已知命题p和q,若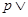 q为假命题,则命题p与q中必一真一假 q为假命题,则命题p与q中必一真一假 |
D.若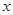 、 、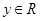 ,则“ ,则“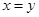 ”是“ ”是“ ”成立的充要条件 ”成立的充要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com