
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() ,且
,且![]() 时,
时,
(i)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(ii)若对任意的![]() ,都有
,都有![]() 成立,求正实数
成立,求正实数![]() 的最大值.
的最大值.
【答案】(1)答案见解析;(2)(i)证明见解析,(ii)4.
【解析】
(1)求导![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,然后分
,然后分![]() ,
,![]() ,
,![]() ,三种情况讨论求解.
,三种情况讨论求解.
(2)(i)求导![]() ,由
,由![]() ,
,![]() 是
是![]() 的两实根,由韦达定理得
的两实根,由韦达定理得![]() ,
,![]() ,构造函数
,构造函数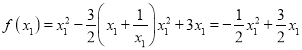 ,利用导数证明即可;(ii)当
,利用导数证明即可;(ii)当![]() 时,不等式恒成立;当
时,不等式恒成立;当![]() 时,将不等式
时,将不等式![]() 转化为
转化为![]() 求解.
求解.
(1)![]() ,
,
![]() .
.
令![]() ,得
,得![]() ,
,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 上递增;
上递增;
②当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() ,
,![]() 上递增,在
上递增,在![]() 递减;
递减;
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() ,
,![]() 上递增,在
上递增,在![]() 上递减.
上递减.
(2)(i)证明:![]() ,
,![]() .
.
由已知![]() ,
,![]() 是方程
是方程![]() ,即
,即![]() 的两实根,
的两实根,
故![]() ,又
,又![]() ,所以
,所以![]() .
.
由韦达定理得:![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,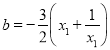 .
.
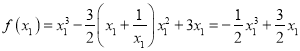 .
.
设![]() ,
,
则![]()
所以![]() 递增,
递增,
故![]() ,即
,即![]() .
.
(ii)当![]() 时,不等式恒成立;
时,不等式恒成立;
当![]() 时,不等式
时,不等式![]() 化为
化为![]() .
.
设![]() ,
,![]()
因为![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() .
.
又![]() ,所以
,所以![]() ,
,
此时![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有( )
A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
B.设有一个线性回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;
平均增加5个单位;
C.设具有相关关系的两个变量![]() ,
,![]() 的相关系数为
的相关系数为![]() ,则
,则![]() 越接近于0,
越接近于0,![]() 和
和![]() 之间的线性相关程度越弱;
之间的线性相关程度越弱;
D.在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,在
的值,在![]() 的前提下,
的前提下,![]() 的值越大,判断两个变量间有关联的把握就越大.
的值越大,判断两个变量间有关联的把握就越大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜食 | 不喜欢甜食 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
附: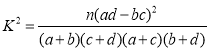
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com