
【题目】已知函数![]() ,若函数
,若函数![]() 在
在![]() 上有两个不同的零点,则实数
上有两个不同的零点,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】
函数可化为:f(x)![]() ,
,
∵若m>0,当0<x<2时,f(x)递增,
当2≤x<3时,f(x)的对称轴是x![]() 0,
0,
故函数f(x)在[2,3)递增,∵f(x)在(0,3)连续,∴f(x)在(0,3)递增;
∴当m>0时,函数f(x)在(0,3)不可能有2个不同的零点,
当m=0时,f(x)![]() 在(0,3)上没有2个不同的零点,
在(0,3)上没有2个不同的零点,
当m<0时,f(x)在(0,2)递减,
①当0![]() 2即﹣8≤m<0时,函数f(x)在[2,3)递增,
2即﹣8≤m<0时,函数f(x)在[2,3)递增,
故函数f(x)在区间(0,3)有2个不同的零点只需满足:
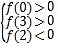 即
即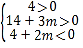 ,解得:
,解得:![]() <m<﹣2,
<m<﹣2,
②当2![]() 3即﹣12<m<﹣8时,
3即﹣12<m<﹣8时,
函数f(x)在(0,![]() )递减,在(
)递减,在(![]() ,3)递增,
,3)递增,
故函数f(x)在区间(0,3)有2个不同的零点只需满足:
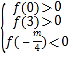 即
即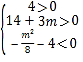 ,解得m>
,解得m>![]() ,又﹣12<m<﹣8,所以不存在满足条件的m,
,又﹣12<m<﹣8,所以不存在满足条件的m,
③当![]() 3即m≤﹣12时,函数f(x)在(0,3)递减,
3即m≤﹣12时,函数f(x)在(0,3)递减,
函数f(x)在(0,3)上不可能有2个不同的零点,
综上,![]() <m<﹣2时,函数f(x)在区间(1,3)上有2个不同的零点.
<m<﹣2时,函数f(x)在区间(1,3)上有2个不同的零点.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及X的数学期望;
及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,![]() .
.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}满足:![]() ,求证:数列{an}为“M-数列”;
,求证:数列{an}为“M-数列”;
(2)已知数列{bn}满足:![]() ,其中Sn为数列{bn}的前n项和.
,其中Sn为数列{bn}的前n项和.
①求数列{bn}的通项公式;
②设m为正整数,若存在“M-数列”{cn}![]() ,对任意正整数k,当k≤m时,都有
,对任意正整数k,当k≤m时,都有![]() 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
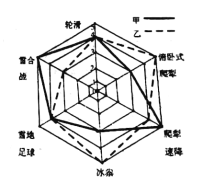
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆E与圆![]() 外切,并与直线
外切,并与直线![]() 相切,记动圆圆心E的轨迹为曲线C.
相切,记动圆圆心E的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线l交曲线C于A,B两点,若曲线C上存在点P使得
的直线l交曲线C于A,B两点,若曲线C上存在点P使得![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() ,且
,且![]() 时,
时,
(i)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(ii)若对任意的![]() ,都有
,都有![]() 成立,求正实数
成立,求正实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com