
【题目】已知![]() ,
,
(1)对![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的最大整数解;
的最大整数解;
(2)令![]() ,若
,若![]() 有两个零点分别为
有两个零点分别为![]() ,
,![]() 且
且![]() 为
为![]() 的唯一的极值点,求证:
的唯一的极值点,求证:![]() .
.
【答案】(1)3 (2)见解析
【解析】
(1)由![]() 等到价于
等到价于![]() ,可令
,可令![]() ,求得导数,再构造函数,求得导数,判断单调性可得
,求得导数,再构造函数,求得导数,判断单调性可得![]() 的单调性,以及最小值,即可得到所求
的单调性,以及最小值,即可得到所求![]() 的最大整数值;
的最大整数值;
(2)求得![]() 的导数的单调性,由极小值小于0,可得
的导数的单调性,由极小值小于0,可得![]() ,再由分析法,注意构造函数,求得导数和单调性,即可得证.
,再由分析法,注意构造函数,求得导数和单调性,即可得证.
(1)解:![]() 等价于
等价于![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为递增函数,
上为递增函数,
因为![]() ,
,
所以存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,
,
所以![]() 的最大整数为3;
的最大整数为3;
(2)证明:![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 的
的![]() 上单调递增,
上单调递增,
此时![]() 不可能有两个零点,
不可能有两个零点,
所以![]() ,
,
所以![]()
解得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
而要使![]() 有两个零点,要满足
有两个零点,要满足![]() ,
,
即![]() ,可得
,可得![]() ,
,
因为![]() ,
,![]() ,令
,令![]() ,
,
由![]() ,得
,得![]()
所以![]() ,
,
而![]()
即![]()
由![]() ,只需证
,只需证![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上递增,
上递增,![]() ;
;
所以![]() 在
在![]() 上递增,
上递增,![]() ,
,
所以![]()


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年3月份,上海出台了《关于建立完善本市生活垃圾全程分类体系的实施方案》,4月份又出台了《上海市生活垃圾全程分类体系建设行动计划(2018-2020年)》,提出到2020年底,基本实现单位生活垃圾强制分类全覆盖,居民区普遍推行生活垃圾分类制度.为加强社区居民的垃圾分类意识,推动社区垃圾分类正确投放,某社区在健身广场举办了“垃圾分类,从我做起”生活垃圾分类大型宣传活动,号召社区居民用实际行动为建设绿色家园贡献一份力量,为此需要征集一部分垃圾分类志愿者.
(1)为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关,现随机选取了一部分社区居民进行调查,其中被调查的男性居民和女性居民人数相同,男性居民中不喜欢担任垃圾分类志愿者占男性居民的![]() ,女性居民中不喜欢担任垃圾分类志愿者占女性居民的
,女性居民中不喜欢担任垃圾分类志愿者占女性居民的![]() ,若研究得到在犯错误概率不超过0.010的前提下,认为居民喜欢担任垃圾分类志愿者与性别有关,则被调查的女性居民至少多少人?
,若研究得到在犯错误概率不超过0.010的前提下,认为居民喜欢担任垃圾分类志愿者与性别有关,则被调查的女性居民至少多少人?
附 ,
,![]() ,
,
| 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(2)某垃圾站的日垃圾分拣量![]() (千克)与垃圾分类志愿者人数
(千克)与垃圾分类志愿者人数![]() (人)满足回归直线方程
(人)满足回归直线方程![]() ,数据统计如下:
,数据统计如下:
志愿者人数 | 2 | 3 | 4 | 6 | |
日垃圾分拣量 | 25 | 30 | 40 | 45 |
|
已知![]() ,
,![]() ,
,![]() ,根据所给数据求
,根据所给数据求![]() 和回归直线方程
和回归直线方程![]() ,附:
,附: ,
,![]() .
.
(3)用(2)中所求的线性回归方程得到与![]() 对应的日垃圾分拣量的估计值
对应的日垃圾分拣量的估计值![]() .当分拣数据
.当分拣数据![]() 与估计值
与估计值![]() 满足
满足![]() 时,则将分拣数据
时,则将分拣数据![]() 称为一个“正常数据”.现从5个分拣数据中任取3个,记
称为一个“正常数据”.现从5个分拣数据中任取3个,记![]() 表示取得“正常数据”的个数,求
表示取得“正常数据”的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.且曲线
轴的正半轴为极轴建立极坐标系.且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院为筛查某种疾病,需要检验血液是否为阳性,现有![]() (
(![]() )份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验
)份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将其中
次;(2)混合检验,将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.若检验结果为阴性,这
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]()
(ⅰ)试运用概率统计的知识,若![]()
![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ⅱ)若![]() ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校数学老师任教的班级有50名学生,某次单元测验成绩的频率分布直方图如图所示,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
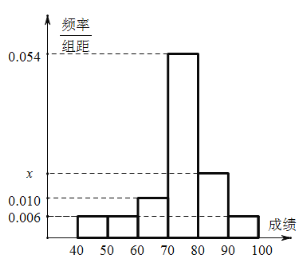
(1)求图中![]() 的值;
的值;
(2)从成绩不低于80分的同学中随机选取3人,该3人中成绩在90分以上(含90分)的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法自古以来就使用的纪年方法,甲、乙、丙、丁、戊、已、庚、辛、壬、癸为十天干;子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥为十二地支.“干支纪年法”是以一个天干和一个地支按上述顺序相配排列起来,天干在前,地支在后,已知2017年是丁酉年,2018年是戊戌年,2019年是已亥年,依此类推,则2080年是____________年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com