
【题目】如图,抛物线![]() 的方程为
的方程为![]() ,已知点
,已知点![]() 、
、![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.

(1)若![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,
,![]() ,根据
,根据![]() 可得出
可得出![]() ,令
,令![]() ,可得出直线
,可得出直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与抛物线的方程联立,列出韦达定理,结合
的方程与抛物线的方程联立,列出韦达定理,结合![]() 可求得正数
可求得正数![]() 的值,由此可得出直线
的值,由此可得出直线![]() 的方程;
的方程;
(2)利用![]() 求得点
求得点![]() 的坐标,并求出
的坐标,并求出![]() 的值,利用两角和的正切公式求得
的值,利用两角和的正切公式求得![]() 的值,可求得
的值,可求得![]() ,利用抛物线的焦点弦长公式可求得
,利用抛物线的焦点弦长公式可求得![]() ,然后利用正弦定理可求得
,然后利用正弦定理可求得![]() 的外接圆半径.
的外接圆半径.
(1)设![]() ,
,![]() ,
,
由于![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,
令![]() ,则直线
,则直线![]() 的方程可化为
的方程可化为![]() ,联立
,联立![]() ,可得
,可得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
所以直线方程为![]() ;
;

(2)由于![]() ,则
,则![]() ,
,
即![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
①当![]() 时,则
时,则![]() ,即点
,即点![]() ,直线
,直线![]() 的斜率为
的斜率为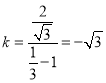 ,不合乎题意;
,不合乎题意;
②当![]() 时,则
时,则![]() ,即点
,即点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,合乎题意.
,合乎题意.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由同角三角函数的基本关系可得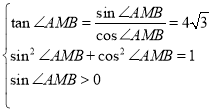 ,解得
,解得![]() ,
,
![]() ,
,
所以![]() 的外接圆半径为
的外接圆半径为![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】某医院为筛查某种疾病,需要检验血液是否为阳性,现有![]() (
(![]() )份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验
)份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将其中
次;(2)混合检验,将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.若检验结果为阴性,这
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]()
(ⅰ)试运用概率统计的知识,若![]()
![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ⅱ)若![]() ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海的国家会展中心举办.国家展、企业展、经贸论坛、高新产品汇集……首届进博会高点纷呈.一个更加开放和自信的中国,正用实际行动为世界构筑共同发展平台,展现推动全球贸易与合作的中国方案.
某跨国公司带来了高端智能家居产品参展,供购商洽谈采购,并决定大量投放中国市场.已知该产品年固定研发成本30万美元,每生产一台需另投入90美元.设该公司一年内生产该产品![]() 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为![]() 万美元,
万美元,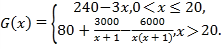
(1)写出年利润![]() (万美元)关于年产量
(万美元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下表格.
(i)请将表格补充完整;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有( )
A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
B.设有一个线性回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;
平均增加5个单位;
C.设具有相关关系的两个变量![]() ,
,![]() 的相关系数为
的相关系数为![]() ,则
,则![]() 越接近于0,
越接近于0,![]() 和
和![]() 之间的线性相关程度越弱;
之间的线性相关程度越弱;
D.在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,在
的值,在![]() 的前提下,
的前提下,![]() 的值越大,判断两个变量间有关联的把握就越大.
的值越大,判断两个变量间有关联的把握就越大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中正确的个数是
(1)对于命题![]() 使得
使得![]() ,则
,则![]() 都有
都有![]() ;
;
(2)已知![]() ,则
,则 ![]()
(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为![]() ;
;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com