
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
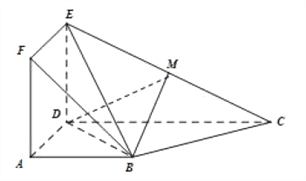
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明过程详见解析;(2)证明过程详见解析;(3)![]() .
.
【解析】
试题本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,作出辅助线MN,N为![]() 中点,在
中点,在![]() 中,利用中位线得到
中,利用中位线得到![]() ,且
,且![]() ,结合已知条件,可证出四边形ABMN为平行四边形,所以
,结合已知条件,可证出四边形ABMN为平行四边形,所以![]() ,利用线面平行的判定,得
,利用线面平行的判定,得![]() ∥平面
∥平面![]() ;第二问,利用面面垂直的性质,判断
;第二问,利用面面垂直的性质,判断![]() 面
面![]() ,再利用已知的边长,可证出
,再利用已知的边长,可证出![]() ,则利用线面垂直的判定得
,则利用线面垂直的判定得![]() 平面BDE,再利用面面垂直的判定得平面
平面BDE,再利用面面垂直的判定得平面![]() 平面
平面![]() ;第三问,可以利用传统几何法证明二面角的平面角,也可以利用向量法建立空间直角坐标系,求出平面BEC和平面ADEF的法向量,利用夹角公式计算即可.
;第三问,可以利用传统几何法证明二面角的平面角,也可以利用向量法建立空间直角坐标系,求出平面BEC和平面ADEF的法向量,利用夹角公式计算即可.
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() .
.

在△![]() 中,
中,
![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ∥
∥![]() ,且
,且
![]() .由已知
.由已知![]() ∥
∥![]() ,
,![]() ,所以
,所以
![]() ∥
∥![]() ,且
,且![]() .所以四边形
.所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ∥
∥![]() .
.
又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(2)证明:在正方形![]() 中,
中,![]() .又因为
.又因为
平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .所以
.所以![]() .
.
在直角梯形![]() 中,
中,![]() ,
,![]() ,可得
,可得![]() .
.
在△![]() 中,
中,![]() ,所以
,所以![]() .
.
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)(方法一)延长![]() 和
和![]() 交于
交于![]() .
.

在平面![]() 内过
内过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .由平面
.由平面![]()
![]() 平面
平面![]() ,
,
![]() ∥
∥![]() ,
,![]() ,平面
,平面![]()
![]() 平面
平面![]() =
=![]() ,
,
得![]() ,于是
,于是![]() .
.
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
于是![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成锐二面角的
所成锐二面角的
平面角.
由![]() ,得
,得![]() .
.
又![]() ,于是有
,于是有![]() .
.
在![]() 中,
中, .
.
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
(方法二)由(2)知![]() 平面
平面![]() ,且
,且![]() .
.
以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]()

易得![]() .平面
.平面![]() 的一个法向量为
的一个法向量为![]() .设
.设![]() 为平面
为平面![]() 的一个法向量,因为
的一个法向量,因为![]() ,
,![]() 所以
所以![]() ,令
,令![]() ,得
,得![]() .
.
所以![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() .
.
则 .所以平面
.所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及X的数学期望;
及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,![]() .
.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆E与圆![]() 外切,并与直线
外切,并与直线![]() 相切,记动圆圆心E的轨迹为曲线C.
相切,记动圆圆心E的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线l交曲线C于A,B两点,若曲线C上存在点P使得
的直线l交曲线C于A,B两点,若曲线C上存在点P使得![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() ,且
,且![]() 时,
时,
(i)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(ii)若对任意的![]() ,都有
,都有![]() 成立,求正实数
成立,求正实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适.②相关指数![]() 来刻画回归的效果,
来刻画回归的效果,![]() 值越大,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )
值越大,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.

(1)估计这次考试的平均分;
(2)假设分数在[90,100]的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,76,97,88,69,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com