
已知数列{2n-1·an}的前n项和Sn=1-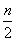 .
.
(1)求数列{an}的通项公式;
(2)设bn= ,求数列
,求数列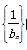 的前n项和.
的前n项和.
解析: (1)由题意可知:Sn-1=1- (n≥2),
(n≥2),
又2n-1·an=Sn-Sn-1,
∴2n-1·an=-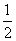 .
.
∴an=-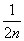 =-2-n(n≥2).∴a1=-
=-2-n(n≥2).∴a1=-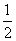 .
.
又S1=1-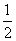 =
=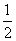 ,
,
∴a1≠S1,
∴an=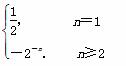
(2)由题意知bn=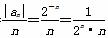 (n≥2),
(n≥2),
∴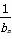 =n·2n(n≥2).
=n·2n(n≥2).
∵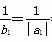 =2,
=2,
∴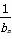 =n·2n(n≥1).
=n·2n(n≥1).
设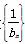 的前n项和为S
的前n项和为S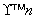 ,
,
则S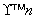 =1×2+2×22+3×23+…+n·2n,
=1×2+2×22+3×23+…+n·2n,
2S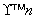 =1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,
=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,
∴S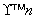 -2S
-2S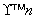 =1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,
=1×2+22+23+…+2n-n·2n+1=2+22+…+2n-n·2n+1,
∴-S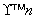 =(1-n)·2n+1-2,
=(1-n)·2n+1-2,
∴S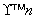 =(n-1)·2n+1+2.
=(n-1)·2n+1+2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
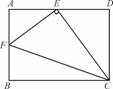
如图,在矩形ABCD中,AB>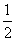 ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设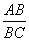 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=|x-a|+3x,其中a>0.
(1) 当a=1时,求不等式f(x)≥3x+2的解集;
(2) 若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an.若a1=1,a2=2,则数列{an}的通项公式是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知⊙P的半径等于6,圆心是抛物线y2=8x的焦点,经过点M(1,-2)的直线l将⊙P分成两段弧,当优弧与劣弧之差最大时,直线l的方程为( )
A.x+2y+3=0 B.x-2y-5=0
C.2x+y=0 D.2x-y-5=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com