
如图,在矩形ABCD中,AB>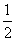 ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设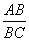 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
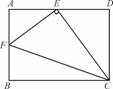
解:假设存在实数k的值,满足题设.
①先证明△AEF∽△DCE∽△ECF.
因为EF⊥EC,
所以∠AEF=90°-∠DEC=∠DCE.
而∠A=∠D=90°,故△AEF∽△DCE.
故得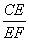 =
=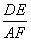 .又DE=EA,所以
.又DE=EA,所以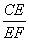 =
=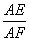 .
.
又∠CEF=∠EAF=90°,
所以△AEF∽△ECF.
②再证明可以取到实数k的值,使△AEF∽△BCF,
由于∠AFE+∠BFC≠90°,故不可能有∠AFE=∠BFC,
因此要使△AEF∽△BCF,应有∠AFE=∠BFC,
此时,有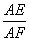 =
=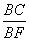 ,又AE=
,又AE=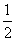 BC,故得AF=
BC,故得AF=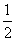 BF=
BF=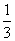 AB.
AB.
由△AEF∽△DCE,可知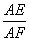 =
=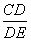 ,
,
因此,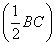
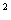 =
=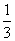 AB2,
AB2,
所以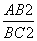 =
=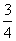 ,求得k=
,求得k=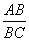 =
=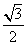 .
.
可以验证,当k=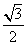 时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知曲线C的极坐标方程为ρ=6sinθ,以极点为原点、极轴为x轴非负半轴建立平面直角坐标系,直线l的参数方程为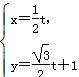 (t为参数),求直线l被曲线C截得的线段的长度.
(t为参数),求直线l被曲线C截得的线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四边形ABCD中,DF⊥AB,垂足为F,DF=3,AF=2FB=2,延长FB到E,使BE=FB.连结BD、EC,若BD∥EC,求△BCD和四边形ABCD的面积.
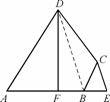
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com