练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=Asin（ωx）+b（A＞0，ω＞0）的最大值为2，最小值为0，其图象相邻两对称轴间的距离为2，则f（1）+f（2）+…+f（2008）= ．

    【答案】2008
    【解析】解：函数f（x）=Asin（ωx）+b（A＞0，ω＞0）的最大值为2，最小值为0， ∴ ，
    A=1，b=1，
    又函数图象相邻两对称轴间的距离为2，∴ = =2，
    ∴ω= ；
    ∴f（1）=（sin +1）=2，
    f（2）=（sinπ+1）=1，
    f（3）=（sin +1）=0，
    f（4）=（sin2π+1）=1；
    f（5）=（sin +1）=2，…；
    ∴f（x）是以4为周期的函数，
    f（1）+f（2）+…+f（2008）=2+1+0+1+…+1=2008．
    所以答案是：2008．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知 与 为互相垂直的单位向量， ， 且 与 的夹角为锐角，则实数λ的取值范围是（ ）
    A.（﹣∞，﹣2）
    B.（ ，+∞）
    C.（﹣2， ）
    D.（﹣ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点（x，y）满足 ，则 的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小王的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：

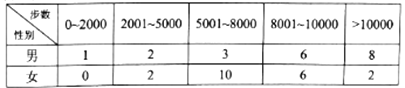
    （1）若采用样本估计总体的方式，试估计小王的所有微信好友中每日走路步数超过5000步的概率；

    （2）已知某人一天的走路步数超过8000步被系统评定“积极型”，否则为“懈怠型”，根据题意完成下面的列联表，并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关？

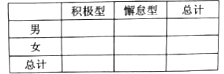    附： ，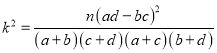

    0．10

    0．05

    0．025

    0．010

    2．706

    3．841

    5．024

    6．635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知极坐标系的极点为直角坐标系的原点，极轴为轴的正半轴，两种坐标系中的长度单位相同，圆的直角坐标方程为，直线的参数方程为（为参数），射线的极坐标方程为．

    （1）求圆和直线的极坐标方程；

    （2）已知射线与圆的交点为，与直线的交点为，求线段的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形，每条侧棱的长都是底面边长的倍，为侧棱上的点．

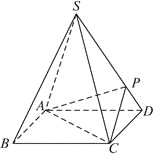
    （1）求证：．

    （2）若⊥平面，求二面角的大小．

    （3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC?若存在，求SE∶EC的值；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= +
    （1）将函数f（x）化简成Asin（ωx+φ）+B（A＞0，φ＞0，φ∈[0，2π））的形式；
    （2）求f（x）的单调递减区间，并指出函数|f（x）|的最小正周期；
    （3）求函数f（x）在[ ， ]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点在以为直径的圆上，垂直与圆所在平面，为的垂心.

    （1）求证：平面平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，BC=2AD，PB⊥AC，Q是线段PB的中点． （Ⅰ）求证：AB⊥平面PAC；
    （Ⅱ）求证：AQ∥平面PCD．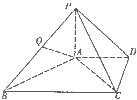

    查看答案和解析>>

    同步练习册答案