
【题目】设![]() 为集合
为集合![]() 的子集,且
的子集,且![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的
的![]() 元“大同集”.
元“大同集”.
(1)写出实数集![]() 的一个二元“大同集”;
的一个二元“大同集”;
(2)是否存在正整数集![]() 的二元“大同集”,请说明理由;
的二元“大同集”,请说明理由;
(3)求出正整数集![]() 的所有三元“大同集”.
的所有三元“大同集”.
【答案】(1)![]() ;(2)不存在,理由详见解析;(3)
;(2)不存在,理由详见解析;(3)![]() .
.
【解析】
(1)利用集合![]() 的
的![]() 元“大同集”的定义能求出实数集
元“大同集”的定义能求出实数集![]() 的一个二元“大同集”.
的一个二元“大同集”.
(2)由两个不同的正整数之和不等于两个不同的正整数之积,得到不存在正整数集![]() 的二元“大同集”.
的二元“大同集”.
(3)设正整数集![]() 的三元“大同集”为
的三元“大同集”为![]() .则
.则![]() ,利用列举法能求出正整数集
,利用列举法能求出正整数集![]() 的所有三元“大同集”.
的所有三元“大同集”.
解:(1)∵设![]() 为集合
为集合![]() 的2元“大同集”.
的2元“大同集”.
则![]() ,
,
当![]() 时,
时,![]() ,得
,得![]()
![]() 实数集
实数集![]() 的一个二元“大同集”为
的一个二元“大同集”为![]() .
.
(2)不存在正整数集![]() 的二元“大同集”,
的二元“大同集”,
![]() 两个不同的正整数之和不可能等于两个不同的正整数之积,
两个不同的正整数之和不可能等于两个不同的正整数之积,
![]() 不存在正整数集
不存在正整数集![]() 的二元“大同集”.
的二元“大同集”.
(3)设正整数集![]() 的三元“大同集”为
的三元“大同集”为![]() .
.
则![]() ,
,
利用列举法得![]() ,
,![]() ,
,![]() 的值分别为1,2,3,
的值分别为1,2,3,
![]() 正整数集
正整数集![]() 的所有三元“大同集”为
的所有三元“大同集”为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
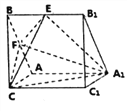
【题目】已知正三棱柱![]() 中,
中, ![]() 分别为
分别为![]() 的中点,设
的中点,设![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求实数
,求实数![]() 的值,并判断此时二面角
的值,并判断此时二面角![]() 是否为直二面角,请说明理由.
是否为直二面角,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程,20项民生类工程和10项产业建设类工程.现有来沈阳的3名工人相互独立地从这60个项目中任选一个项目参与建设.
(Ⅰ)求这3人选择的项目所属类别互异的概率;
(Ⅱ)将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为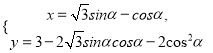 (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 和曲线
和曲线![]() 的交点
的交点![]() 的直角坐标;
的直角坐标;
(2)当![]() 时,设
时,设![]() ,
, ![]() 分别是曲线
分别是曲线![]() 与曲线
与曲线![]() 上动点,求
上动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后抛掷两枚骰子,设出现的点数之和是12,11,10的概率依次是P1,P2,P3,则( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
![]() ,
, ![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,写出相应的集合
的集合,写出相应的集合![]() 和
和![]() .
.
(Ⅱ)对任何具有性质![]() 的集合
的集合![]() ,证明
,证明![]() .
.
(Ⅲ)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
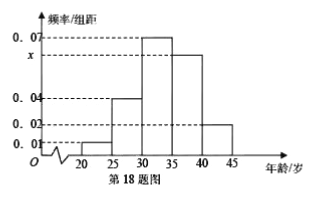
【题目】为增强市民的节能环保意识,汕头市面向全市征召义务宣传志愿者,从符合条件的 500 名志愿者中随机抽取 100 名,其年龄频率分布直方图如图所示,其中年龄分组区是:
![]() ,
,
(1)求图中![]() 的值,并根据频率分布直方图估计这 500 名志愿者中年龄在
的值,并根据频率分布直方图估计这 500 名志愿者中年龄在![]() 岁的人数;
岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 10 名参加人民广场的宣传活动,再从这 10 名志愿者中选取 3 名担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 ![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com