
 的底面
的底面 是矩形,
是矩形, 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 ,
, ,
,
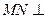 平面
平面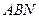
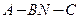 的余弦值
的余弦值
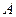 点为原点,
点为原点,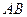 为
为
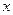 轴,
轴,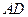
 为
为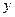 轴,
轴,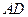 为
为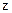 轴的空间直角坐标系,如图所示.则依题意可知相关各点的坐标分别是:
轴的空间直角坐标系,如图所示.则依题意可知相关各点的坐标分别是: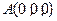 ,
,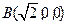 ,
,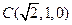 ,
,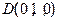 ,
,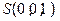 如下图所示.………………………………………………………
如下图所示.……………………………………………………… ……………………(2分)
……………………(2分)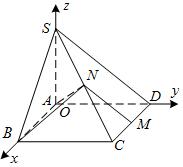
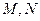 点的坐标分别为
点的坐标分别为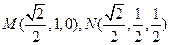 ……………………………
…………………………… ……………(3分)
……………(3分)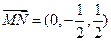 ,
,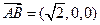 ,
,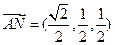 ......................... (4分)
......................... (4分)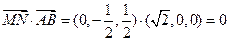 ,所以
,所以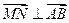 .......................... (6分)
.......................... (6分)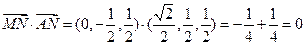 ,所以
,所以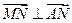 .............. (7分)
.............. (7分)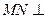 平面
平面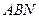 ........................................................... (8分)
........................................................... (8分)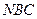 的法向量
的法向量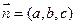 ,则
,则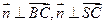 ,........................ (9分)
,........................ (9分)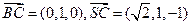
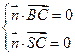
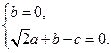 ............................................................. (10分)
............................................................. (10分)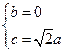
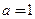 ,则
,则
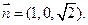
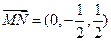 就是平面
就是平面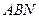 的法向量................................... (11分)
的法向量................................... (11分)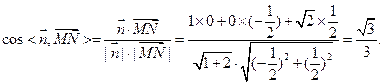 .................... (12分)
.................... (12分)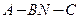 是钝角二面角........................................ (13分)
是钝角二面角........................................ (13分)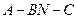 的余弦值为
的余弦值为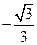 .......................................... (14分)
.......................................... (14分)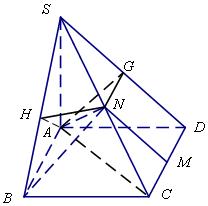
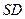 的中点
的中点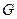 ,连接
,连接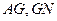 ,则
,则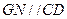 ,又
,又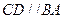 ,所以四点
,所以四点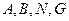 共面.
共面.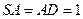 ,且
,且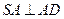 .......... (2分)]
.......... (2分)]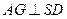 .
.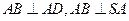 ,
,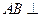 平面
平面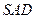 ..................... (4分)
..................... (4分)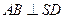
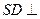 平面
平面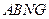 ................... (6分)
................... (6分)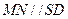
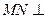 平面
平面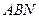 ................... (8分)
................... (8分)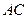 ,则
,则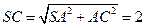
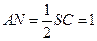 .............................................................. (9分)
.............................................................. (9分)
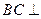 平面
平面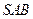 .
.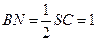 ,且平面
,且平面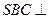 平面
平面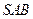 .
.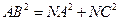 ,所以
,所以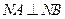 ........................................... (10分)
........................................... (10分)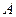 作
作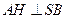 ,垂足为
,垂足为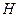 ,则
,则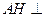 平面
平面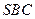 .
.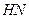 ,则
,则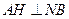 ......................................................... (11分)
......................................................... (11分)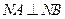 ,
,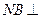 平面
平面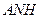 ,
,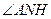 为二面角
为二面角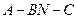 平面角的补角. ....................................... (12分)
平面角的补角. ....................................... (12分)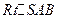 中,
中,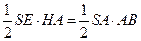 ,所以
,所以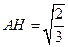 .
.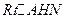 中,
中,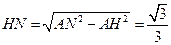
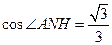 ........................................................... (13分)
........................................................... (13分)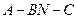 的余弦值为
的余弦值为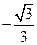 .......................................... (14分)
.......................................... (14分)

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
, ,则
,则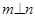 ②若
②若 ,
, ,
, ,则
,则
 ,
, ,则
,则 ④若
④若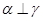 ,
, ,则
,则
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com