
 如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转过程中的一个图形.现给出下列命题:
如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转过程中的一个图形.现给出下列命题:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据线面平行的判定定理,由BC∥DE,可得直线BC∥平面A′DEG,故①正确;根据线面垂直的判定定理,由DE⊥A′G,DE⊥FG,可得直线DE⊥平面A′FG,故②正确;根据面面垂直的判定定理,由直线DE⊥平面A′FG,DE?平面A′DE,可得恒有平面A′FG⊥平面A′DE,故③正确.
解答 解:对于①:∵BC∥DE,DE?面A'DE,BC?面A'DE,∴BC∥面A'DE.故①正确;
对于②:∵△ABC是正三角形,F为BC的中点,∴DE⊥AF,∴DE⊥A'G,DE⊥FG,又∵A'G∩FG=G,
∴DE⊥平面A′FG.故②正确;
对于③:由②可知,DE⊥平面A′FG,又∵DE?平面A′DE,∴平面A′FG⊥平面A′DE.故③正确.
综上可得,正确命题的个数为3个
故选:D
点评 本题主要考查了立体几何中线线、线面、面面的位置关系,需熟练掌握线面平行的判定定理,线面垂直的判定定理,面面垂直的判定定理.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,3) | B. | (6,7] | C. | [6,7) | D. | [9,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
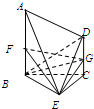 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n⊥α,则m∥α | B. | 若α⊥β,m∥α,则m⊥β | ||
| C. | 若m∥α,n∥β,m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com