
【题目】将7名应届师范大学毕业生分配到3所中学任教.
(1)4个人分到甲学校,2个人分到乙学校,1个人分到丙学校,有多少种不同的分配方案?
(2)一所学校去4个人,另一所学校去2个人,剩下的一个学校去1个人,有多少种不同的分配方案?
科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
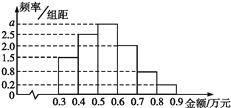
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
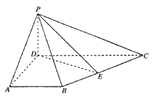
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】媒体为调查喜欢娱乐节目![]() 是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
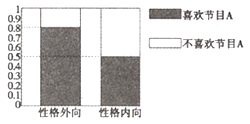
(1)填写完整如下![]() 列联表;
列联表;

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.001的前提下认为喜欢娱乐节目![]() 与性格外向有关?
与性格外向有关?
参考数据及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
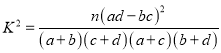
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com