
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
【答案】(1)增区间为![]() ;(2)
;(2)![]() ;(3)
;(3) .
.
【解析】试题分析:(1)根据奇偶性,结合函数简图可得函数的增区间;(2)因为![]() ,
, ![]() ,所以根据函数
,所以根据函数![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数, ![]() , 且当
, 且当![]() 时,
时, ![]() ,
, ![]() 时函数
时函数![]() 的解析式,综合可得函数
的解析式,综合可得函数![]() 的解析式;(3)根据(1)可得函数
的解析式;(3)根据(1)可得函数![]() 的解析式,结合二次函数的图象和性质,对
的解析式,结合二次函数的图象和性质,对![]() 进行分类讨论,进而可得函数
进行分类讨论,进而可得函数![]() 的最小值的表达式.
的最小值的表达式.
试题解析:(1)![]() 的增区间为
的增区间为![]() .
.
(2)设![]() ,则
,则![]() ,
,![]()
![]() ,
,
由已知![]() ,
,![]() 当
当![]() 时,
时,![]() ,故函数
,故函数![]() 的解析式为:
的解析式为: .
.
(3)由(2)可得:![]() ,对称轴为:
,对称轴为:![]() ,
,
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递增,故
上单调递增,故![]() 的最小值为
的最小值为![]() ,
,
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 在对称轴处取得最小值,故
在对称轴处取得最小值,故![]() 的最小值为
的最小值为![]() ,
,
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递减,故
上单调递减,故![]() 的最小值为
的最小值为![]() .
.
综上:所求最小值为![]()
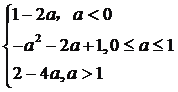 .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发, ![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
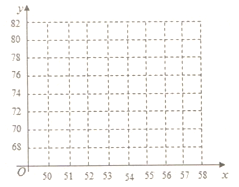
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式: 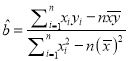
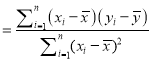 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ).
).
(1)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的极值点;
的极值点;
(3)令![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上相异三点,其中
上相异三点,其中![]() .求证:
.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将7名应届师范大学毕业生分配到3所中学任教.
(1)4个人分到甲学校,2个人分到乙学校,1个人分到丙学校,有多少种不同的分配方案?
(2)一所学校去4个人,另一所学校去2个人,剩下的一个学校去1个人,有多少种不同的分配方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

(1)令![]() ,利用给出的参考数据求出
,利用给出的参考数据求出![]() 关于
关于![]() 的回归方程
的回归方程![]() .(
.(![]() ,
,![]() 精确到0.1)
精确到0.1)
参考数据:![]() ,
,![]() ,
,![]()
其中![]() ,
,![]()
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
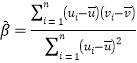 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com