
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.

【答案】(Ⅰ)T=![]() .(Ⅱ)下一个销售季度的利润T不少于57000元的概率的估计值为0.7.
.(Ⅱ)下一个销售季度的利润T不少于57000元的概率的估计值为0.7.
【解析】试题分析:(I)由题意先分段写出,当X∈[100,130)时,当X∈[130,150)时,和利润值,最后利用分段函数的形式进行综合即可.
(II)由(I)知,利润T不少于57000元,当且仅当120≤X≤150.再由直方图知需求量X∈[120,150]的频率为0.7,利用样本估计总体的方法得出下一个销售季度的利润T不少于57000元的概率的估计值.
解:(I)由题意得,当X∈[100,130)时,T=500X﹣300(130﹣X)=800X﹣39000,
当X∈[130,150]时,T=500×130=65000,
∴T=![]() .
.
(II)由(I)知,利润T不少于57000元,当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,
所以下一个销售季度的利润T不少于57000元的概率的估计值为0.7.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家里躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》.自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求:“幼儿园、中小学等教育机构停课,停课不停学”,学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的.某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)请补全被调查人员年龄的频率分布直方图;
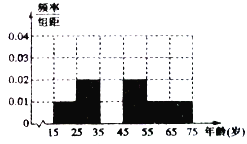
(2)若从年龄在![]() 的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
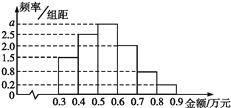
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
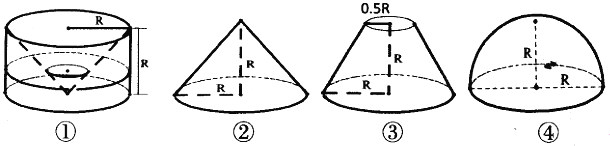
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
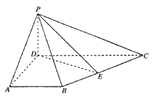
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产![]() ,
, ![]() 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产![]() 类产品5件和
类产品5件和![]() 类产品10件,乙种设备每天能生产
类产品10件,乙种设备每天能生产![]() 类产品6件和
类产品6件和![]() 类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产
类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产![]() 类产品50件,
类产品50件, ![]() 类产品140件,则所需租赁费最少为__________元.
类产品140件,则所需租赁费最少为__________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com