【题目】某公司租赁甲、乙两种设备生产
， 
两类产品，甲种设备每天能生产
类产品5件和
类产品10件，乙种设备每天能生产
类产品6件和
类产品20件.已知设备甲每天的租赁费为300元，设备乙每天的租赁费为400元，现该公司至少要生产
类产品50件， 
类产品140件，则所需租赁费最少为__________元．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案科目：高中数学 来源： 题型：
【题目】经销商经销某种农产品，在一个销售季度内，每售出
该产品获利润500元，未售出的产品，每
亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直图，如图所示．经销商为下一个销售季度购进了
该农产品．以
（
）表示下一个销售季度内的市场需求量， 
（单位：元）表示下一个销售季度内经销该农产品的利润．
（Ⅰ）将
表示为
的函数；
（Ⅱ）根据直方图估计利润
不少于57000元的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），在以
为极点， 
轴的正半轴为极轴的极坐标系中，曲线
是圆心在极轴上，且经过极点的圆.已知曲线
上的点
对应的参数
，射线
与曲线
交于点
.
（Ⅰ）求曲线
的直角坐标方程；
（Ⅱ）若点
， 
在曲线
上，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学从参加高一年级上学期期末考试的学生中抽出60名学生，将其成绩(均为整数)分成六段[40，50)，[50，60)，…，[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
(1)估计这次考试的及格率(60分及以上为及格).
(2)从成绩是70分以上(包括70分)的学生中选一人，求选到第一名学生的概率(第一名学生只一人).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
： 
的离心率为
， 
为椭圆
的右焦点， 
， 
.
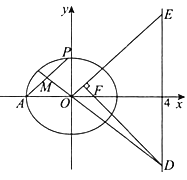
（Ⅰ）求椭圆
的方程；
（Ⅱ）设
为原点， 
为椭圆上一点， 
的中点为
，直线
与直线
交于点
，过
作
，交直线
于点
，求证： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水
（单位：千克）清洗该蔬菜1千克后，蔬菜上残留的农药
（单位：微克）的统计表：
（1）令
，利用给出的参考数据求出关于
的回归方程
.（
，
精确到0.1）
参考数据：
，
，
其中
，
（2）对于某种残留在蔬菜上的农药，当它的残留量不高于20微克时对人体无害，为了放心食用该蔬菜，请估计至少需用用多少千克的清水清洗1千克蔬菜？（精确到0.1，参考数据
）
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
.
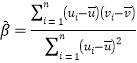查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
，（ 
为常数）
（1）若
在
处的切线方程为
（
为常数），求
的值；
（2）设函数
的导函数为
，若存在唯一的实数
，使得
与
同时成立，求实数
的取值范围；
（3）令
，若函数
存在极值，且所有极值之和大于
，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某教师有相同的语文参考书3本，相同的数学参考书4本，从中取出4本赠送给4位学生，每位学生1本，则不同的赠送方法共有（ ）
A. 15种 B. 20种 C. 48种 D. 60种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
