
分析 本题属导数简单综合题;(1)首先对f(x)求导,利用f'(x)>0与f'(x)<0来判断原函数的单调区间;
(2)构造新函数h(x)=f(x)-g(x),利用导数方法求函数h(x)在区间上的最大值h(1)<0,从而得证.
解答 解:(1)f(x)的定义域是(0,+∞),
当a=-1时,f'(x)=x-$\frac{1}{x}$=$\frac{(x+1)(x-1)}{x}$;
当x∈(0,1)时,f'(x)<0,所以f(x)在(0,1)上递减;
当x∈(1,+∞)时,f'(x)>0,所以f(x)在(1,+∞)上递增;
所以,f(x)在(0,1)单调递减,(1,+∞)上单调递增.
(2)证明:f(x)=$\frac{1}{2}{x}^{2}+lnx$
令h(x)=f(x)-g(x)=$\frac{1}{2}{x}^{2}$+lnx-$\frac{2}{3}{x}^{3}(x≥1)$
h'(x)=x+$\frac{1}{x}-2{x}^{2}$=-$\frac{(x-1)(2{x}^{2}+x+1)}{x}≤0$在[1,+∞)上恒成立,
∴h(x) 在区间[1,+∞)上递减,
∴h(x)≤h(1)=-$\frac{1}{6}<0$
∴在区间[1,+∞)上,函数f(x)的图象在g(x)=$\frac{2}{3}{x}^{3}$的图象下方.
点评 本题主要考查了导数单调性以及构造函数在导数综合题中的应用,属中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| n | 二进制数 | an | n | 二进制数 | an | n | 二进制数 | an |
| 1 | 1 | 2 | 6 | 110 | 4 | 11 | 1011 | 8 |
| 2 | 10 | 2 | 7 | 111 | 8 | 12 | 1100 | 4 |
| 3 | 11 | 4 | 8 | 1000 | 2 | 13 | 1101 | 8 |
| 4 | 100 | 2 | 9 | 1001 | 4 | 14 | 1110 | 8 |
| 5 | 101 | 4 | 10 | 1010 | 4 | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
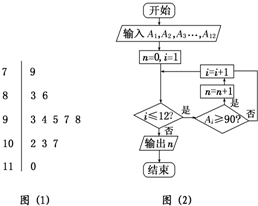 图(1)是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第12次的考试成绩依次记为A1,A2,…,A12.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个程序框图.那么输出的结果是9.
图(1)是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第12次的考试成绩依次记为A1,A2,…,A12.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个程序框图.那么输出的结果是9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com