
【题目】已知数列![]() 的首项
的首项![]() ,其前
,其前![]() 项和为
项和为![]() ,对于任意正整数
,对于任意正整数![]() ,
,![]() ,都有
,都有![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 满足
满足![]() ,且
,且![]() .
.
①求证数列![]() 为常数列.
为常数列.
②求数列![]() 的前
的前![]() 项和
项和![]() .
.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.?x,y∈R,若x+y≠0,则x≠1且y≠﹣1
B.a∈R,“ ![]() ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0”
D.设随机变量X~N(1,52),若P(X<0)=P(X>a﹣2),则实数a的值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB= ![]() .
. 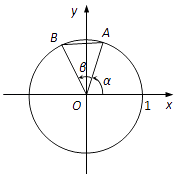
(1)求cosβ的值;
(2)若点A的横坐标为 ![]() ,求点B的坐标.
,求点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
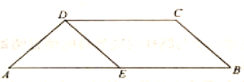
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
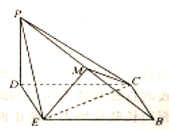
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆心角为![]() ,半径为
,半径为![]() 的扇形铁皮上截取一块矩形材料
的扇形铁皮上截取一块矩形材料![]() ,其中点
,其中点![]() 为圆心,点
为圆心,点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铁皮
在两半径上,现将此矩形铁皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱形铁皮罐的容积为
,圆柱形铁皮罐的容积为![]() .
.

(1)求圆柱形铁皮罐的容积![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当![]() 为何值时,才使做出的圆柱形铁皮罐的容积
为何值时,才使做出的圆柱形铁皮罐的容积![]() 最大?最大容积是多少? (圆柱体积公式:
最大?最大容积是多少? (圆柱体积公式:![]() ,
,![]() 为圆柱的底面枳,
为圆柱的底面枳,![]() 为圆柱的高)
为圆柱的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com