
分析 问题转化为a>$\frac{{e}^{x}+x-1}{{e}^{-x}-x-1}$,设h(x)=$\frac{{e}^{x}+x-1}{{e}^{-x}-x-1}$,利用极限的思想求出函数h(x)的最大值,问题得以解决.
解答 解:∵f(x)=ex-ae-x+(a+1)x+a-1,对于任意的x∈(0,+∞),都有f(x)>0,
∴ex+x-1>a(e-x-x-1),
∵g(x)=e-x-x-1在(0,+∞)为减函数,
∴g(x)max<g(0)=0,
∴g(x)<0,
∴a>$\frac{{e}^{x}+x-1}{{e}^{-x}-x-1}$
设h(x)=$\frac{{e}^{x}+x-1}{{e}^{-x}-x-1}$,
∴$\underset{lim}{x→0}$=$\frac{{e}^{x}+x-1}{{e}^{-x}-x-1}$=$\underset{lim}{x→0}$=$\frac{{e}^{x}}{-{e}^{-x}}$=-1,
∴a≥-1,
故a的取值范围为[-1,+∞).
点评 本题考查了参数的取值范围以及函数恒成立的问题和极限的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
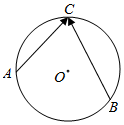 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com