
分析 根据分式函数的性质结合基本不等式的性质进行分解求解即可得函数的值域,根据不等式恒成立转化为求函数的最值问题即可得到结论.
解答 解:f(x)=$\frac{{x}^{2}+3}{|x-1|}$=$\frac{(x-1)^{2}+2(x-1)+4}{|x-1|}$=|x-1|+$\frac{2(x-1)}{|x-1|}$+$\frac{4}{|x-1|}$,
若x>1,则f(x)=(x-1)+$\frac{4}{x-1}$+2≥2$\sqrt{(x-1)•\frac{4}{x-1}}$+2=4+2=6,当且仅当x-1=$\frac{4}{x-1}$,即x-1=2,x=3时取等号,
若x<1,则f(x)=-(x-1)-$\frac{4}{x-1}$-2=1-x+$\frac{4}{1-x}$-2≥2$\sqrt{(1-x)•\frac{4}{1-x}}$-2=4-2=2,当且仅当-(x-1)=-$\frac{4}{x-1}$,即1-x=2,x=-1时取等号,
综上f(x)≥2,即函数f(x)的值域为[2,+∞),
若对任意的x1,x2∈R,均有f(x1)≥g(x2),
则等价为f(x)min≥g(x)max,
即2≥g(x)恒成立,
即2≥1+kcosx,即kcosx≤1,
若k=0,不等式成立,
若k>0,则不等式等价为cosx≤$\frac{1}{k}$,
即1≤$\frac{1}{k}$,则0<k≤1,
若k<0,则不等式等价为cosx≥$\frac{1}{k}$,
即-1≥$\frac{1}{k}$,则-1≤k<0,
综上-1≤k≤1,
故答案为:[2,+∞),[-1,1]
点评 本题主要考查函数值域的求解以及函数最值的应用,利用参数分离法转化为求函数的最值问题是解决本题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
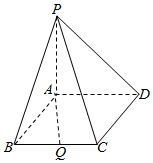 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,四边形ABCD是菱形,并且PA=3,AB=2,∠ABC=60°,点Q为BC中点.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,四边形ABCD是菱形,并且PA=3,AB=2,∠ABC=60°,点Q为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
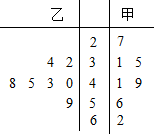 某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示:
某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ③④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 945 | B. | -945 | C. | 1024 | D. | -1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com