
 ij����������ҵ��ij�ؼ��ж�����������������һ�����˵꣬������2015���1��7�·ݵ�����y����λ����Ԫ���羥Ҷͼ��ʾ��
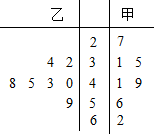
ij����������ҵ��ij�ؼ��ж�����������������һ�����˵꣬������2015���1��7�·ݵ�����y����λ����Ԫ���羥Ҷͼ��ʾ������ ��1������ס������������ƽ��������������Ҷͼ�е�������ɢ��������ɵó����ۣ�
��2�������������ݣ����X�Ŀ���ȡֵ�Լ���Ӧ�ĸ��ʣ��г�X�ķֲ��У�������ѧ����ֵ��
��3���жϼ������y���·�t������ع�ϵ�����ù�ʽ������Իع鷽�̣���Ԥ�������С��
��� �⣺��1�������㣬�������ƽ��ˮƽΪ43���ҵ������ƽ��ˮƽҲΪ43��
���Ӿ�Ҷͼ���ҵ�����ݱȽϼ��У�������ݱȽϷ�ɢ��
��2���ɱ�֪��14�������У�����45����5����X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$\frac{{C}_{9}^{2}}{{C}_{14}^{2}}$=$\frac{36}{91}$��P��X=1��=$\frac{{C}_{5}^{1}{•C}_{9}^{1}}{{C}_{14}^{2}}$=$\frac{45}{91}$��
P��X=2��=$\frac{{C}_{5}^{2}}{{C}_{14}^{2}}$=$\frac{10}{91}$��
����X�ķֲ���Ϊ��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{36}{91}$ | $\frac{45}{91}$ | $\frac{10}{91}$ |
���� ���⿼���˾�Ҷͼ����ɢ����������ֲ��С���ѧ������Ӧ�����⣬Ҳ���������Իع鷽�̵�Ӧ�����⣬���ۺ�����Ŀ��


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22016 | B�� | -22016 | C�� | 22016i | D�� | -22016i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
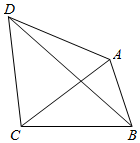 ��ͼ��ʾ��ƽ���ı���ABCD�У�AB=1��BC=2����ACDΪ�������Σ����BCD����������ֵΪ$\sqrt{3}$+1��
��ͼ��ʾ��ƽ���ı���ABCD�У�AB=1��BC=2����ACDΪ�������Σ����BCD����������ֵΪ$\sqrt{3}$+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
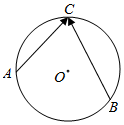 ��ͼ����O����OΪԲ�ġ�1Ϊ�뾶��Բ�����A��B��CΪ��O�ϵ��������㣬��$\overrightarrow{AC}$•$\overrightarrow{BC}$��ȡֵ��ΧΪ[-4��4]��
��ͼ����O����OΪԲ�ġ�1Ϊ�뾶��Բ�����A��B��CΪ��O�ϵ��������㣬��$\overrightarrow{AC}$•$\overrightarrow{BC}$��ȡֵ��ΧΪ[-4��4]���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com