
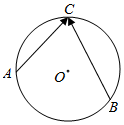
 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4]. 分析 不妨设圆的方程为x2+y2=1,C(1,0),A(cosα,sinα),B(cosβ,sinβ),运用向量的数量积的坐标表示,以及二倍角的余弦公式和和差化积公式,结合正弦函数和余弦函数的值域,即可得到所求范围.
解答 解:不妨设圆的方程为x2+y2=1,
C(1,0),A(cosα,sinα),B(cosβ,sinβ),
则$\overrightarrow{AC}$•$\overrightarrow{BC}$=(1-cosα,-sinα)•(1-cosβ,-sinβ)
=1-cosα-csβ+cosαcosβ+sinαsinβ
=1+cos(α-β)-2cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$
=2cos2$\frac{α-β}{2}$-2cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$
=2cos$\frac{α-β}{2}$(cos$\frac{α-β}{2}$-cos$\frac{α+β}{2}$)
=4cos$\frac{α-β}{2}$sin$\frac{α}{2}$sin$\frac{β}{2}$,
当α=4kπ+π,β=4lπ+π,α-β=4mπ,k,l,m∈Z时,取得最大值4;
当α=4kπ-π,β=4lπ-π,α-β=4mπ+2π,k,l,m∈Z时,取得最小值-4.
综上可得,$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围是[-4,4].
故答案为:[-4,4].
点评 本题考查向量的数量积的坐标表示,考查圆的参数方程的运用,考查三角函数的化简和求值,注意运用正弦函数和余弦函数的值域,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
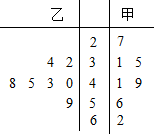 某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示:
某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 32 34 32 | B. | 33 45 35 | C. | 34 45 32 | D. | 33 36 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com