练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:

     
         		男生
         		女生
         		合计
     
      收看
         		    10
         		 
         		 
     
     不收看
         		 
         		   8
         		 
     
    合计
         		 
         		 
         		  30
     
     
    已知在这30名同学中随机抽取1人，抽到“通过电视收看世界杯”的学生的概率是.
    (I)请将上面的列联表补充完整,并据此资料分析“通过电视收看世界杯”与性别是否有关?
    (II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.

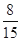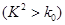         		  0.100
         		0.050
         		0.010
     

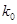         		2.706
         		3.841
         		6.635
     
     
    (参考公式：， )

    (Ⅰ)没有充足的理由认为“通过电视收看世界杯”与性别有关 ；（Ⅱ）．

    解析试题分析：
    解题思路：(Ⅰ)补充表格，套用公式求值，利用临界值表进行判定；（Ⅱ）利用超几何分布的概率公式求概率，再进一步求数学期望.
    规律总结：1.利用独立性检验思想判断两个变量间的相关关系，要牢记公式与临界值表；2.利用概率或随机变量的分布列以及期望、方差解决应用题时，要注意随机变量的实际意义.
    试题解析：(Ⅰ)

     
    		男生
    		女生
    		合计
    收看
    		10
    		6
    		16
    不收看
    		6
    		8
    		14
    合计
    		16
    		14
    		30
     
    由已知数据得:
    所以,没有充足的理由认为“通过电视收看世界杯”与性别有关 .
    (Ⅱ)的可能取值为 
    ，     
    所以的分布列为:

    		0
    		1
    		2




     
    的均值为:
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

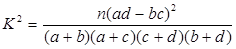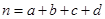    科目：高中数学 来源： 题型：解答题

    高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
    （1）若成绩大于等于14秒且小于16秒规定为良好，求该班在这次百米测试中成绩为良好的人数．
    （2）请根据频率分布直方图，估计样本数据的众数和中位数（精确到0.01）．
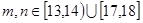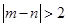    (3)设表示该班两个学生的百米测试成绩，已知，求事件的概率.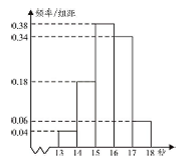

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，（阴影部分为破坏部分）其可见部分如下，据此解答如下问题：
     
    （Ⅰ）计算频率分布直方图中[80,90)间的矩形的高；
    （Ⅱ）若要从分数在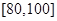之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份的分数在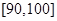之间的概率；
    （Ⅲ）根据频率分布直方图估计这次测试的平均分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

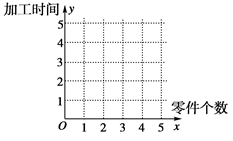
    某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

    零件的个数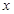（个）
    		2
    		3
    		4
    		5
    加工的时间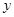（小时）
    		2.5
    		3
    		4
    		4.5
     
    （1）在给定的坐标系中画出表中数据的散点图；
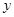    （2）求出关于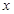的线性回归方程，并在坐标系中画出回归直线；
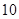    （3）试预测加工个零件需要多少时间？
    参考公式：回归直线，其中.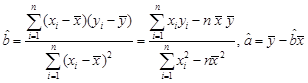

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时)，共有2000人参加调查,现将数据整理分组后如题中表格所示.

    序号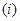

    		分组睡眠时间
    		组中值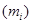

    		频数
    (人数)
    		频率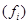
    1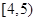

    		4.5
    		80
    		 (    )
    2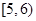

    		5.5
    		520
    		0.26
    3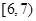

    		6.5
    		600
    		0.30
    4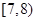

    		7.5
    		(    )
    		(    )
    5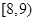

    		8.5
    		200
    		0.10
    6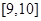

    		9.5
    		40
    		0.02
     
    （1）求出表中空白处的数据，并将表格补充完整；
    （2）画出频率分布直方图；
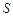    （3）为了对数据举行分析，采用了计算机辅助计算.分析中一部分计算见算法流程图，求输出的值。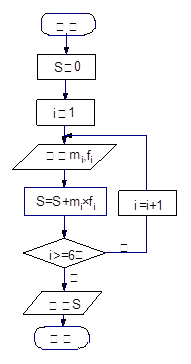

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查，
    统计数据如下表所示：

     
    		积极参加班级工作
    		 不太积极参加班级工作
    		合计
    学习积极性高
    		      18
    		       7
    		 25
    学习积极性一般
    		       6
    		       19
    		 25
    合计
    		      24
    		       26
    		 50
     
    试运用独立性检验的思想方法分析：学生的学习积极性与对待班级的态度是否有关系？

    2

     
    说明理由。

    附：K2=
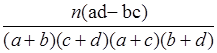
    P(K2≥k0 )
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001
       k0
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    近年来，我国很多城市都出现了严重的雾霾天气．为了更好地保护环境，2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:

    组别
    		 PM2.5浓度（微克/立方米）
    		频数（天）
    第一组
    		（0,35]
    		24
    第二组
    		(35,75]
    		48
    第三组
    		(75,115]
    		12
    第四组
    		>115
    		6
     
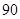    （1）在这天中抽取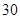天的数据做进一步分析,每一组应抽取多少天?
    （2）在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    从某小学随机抽取100名同学，将他们身高（单位：厘米）数据绘制成频率分布直方图（如图）。由图中数据可知a=         。若要从身高在[120，130﹚，[130，140﹚，[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为         。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    把容量是100的样本分成8组，从第1组到第4组的频数分别是15，17，11，13，第5组到第7组的频率之和是0.32，那么第8组的频率是         .

    查看答案和解析>>

    同步练习册答案