
【题目】已知定义在R上的函数![]() 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的![]() ,都有
,都有![]() ;②对于任意的
;②对于任意的![]() 都有
都有![]() ③函数
③函数![]() 的图象关于y轴对称,则下列结论中正确的是( )
的图象关于y轴对称,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
由①可知函数f(x)是周期T=4的周期函数; 由②可得函数f(x)在[0,2]上单调递增;由③可得函数f(x)的图象关于直线x=2对称.于是f(4.5)=f(0.5),f(7)=f(3)=f(1),f(6.5)=f(2.5)=f(1.5).即可得出结果.
定义在R上的函数y=f(x)满足以下三个条件:由①对于任意的x∈R,都有f(x+4)=f(x),可知函数f(x)是周期T=4的周期函数; ②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2),可得函数f(x)在[0,2]上单调递增;③函数y=f(x+2)的图象关于y轴对称,可得函数f(x)的图象关于直线x=2对称.∴f(4.5)=f(0.5),f(7)=f(3)=f(1),f(6.5)=f(2.5)=f(1.5).∵f(0.5)<f(1)<f(1.5),∴f (4.5)<f (7)<f (6.5).
故选:B.


科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁).其猜对歌曲名称与否的人数如图所示.
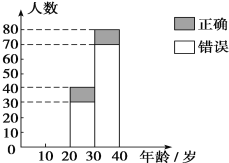
(1)写出2×2列联表;判断能否在犯错误的概率不超过0.10的前提下认为猜对歌曲名称与年龄有关系,说明你的理由.(下面的临界值表供参考)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,求20~30岁与30~40岁各有几人.
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:![]() ,并绘制出频率分布直方图,如图所示.
,并绘制出频率分布直方图,如图所示.
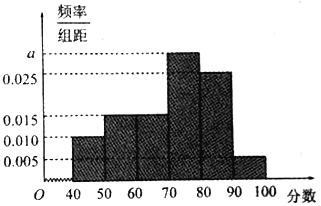
(1)求频率分布直方图中![]() 的值,并估计该市高中学生的平均成绩;
的值,并估计该市高中学生的平均成绩;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 四名学生的考试成绩在区间
四名学生的考试成绩在区间![]() 内,
内,![]() 、
、![]() 两名学生的考试成绩在区间
两名学生的考试成绩在区间![]() 内,现从这6名学生中任选两人参加座谈会,求学生
内,现从这6名学生中任选两人参加座谈会,求学生![]() 、
、![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() ;当
;当![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的值.
的值.
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.离散型随机变量![]() 的方差
的方差![]() 反映了随机变量
反映了随机变量![]() 取值的波动情况;
取值的波动情况;
B.随机变量![]() ,其中
,其中![]() 越小,曲线越“矮胖”;
越小,曲线越“矮胖”;
C.若![]() 与
与![]() 是相互独立事件,则
是相互独立事件,则![]() 与
与![]() 也是相互独立事件;
也是相互独立事件;
D.从10个红球和20个白球除颜色外完全相同中,一次摸出5个球,则摸到红球的个数服从超几何分布;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com