
【题目】试求出正整数![]() 的最小可能值,使得下述命题成立:对于任意的
的最小可能值,使得下述命题成立:对于任意的![]() 个整数
个整数![]() (允许相等),必定存在相应的
(允许相等),必定存在相应的![]() 个整数
个整数![]() (也允许相等),且
(也允许相等),且![]() ,
,![]() ,使得2003能整除
,使得2003能整除![]() .
.
【答案】7
【解析】
先证明![]() 时,命题成立.为此,考虑和式
时,命题成立.为此,考虑和式![]() ,其中
,其中![]() .
.
这种和式共有![]() 个,由于
个,由于![]() ,所以,由抽屉原则可知,必有两个不同的和式
,所以,由抽屉原则可知,必有两个不同的和式![]() 与
与![]() 被2003除所得的余数相同.
被2003除所得的余数相同.
故2003能整除![]()
![]() .
.
其中![]() ,
,![]() (因为
(因为![]() 、
、![]() ,
,![]() ),且至少有一个
),且至少有一个![]() (因为数组
(因为数组![]() ).这时,取
).这时,取![]() ,
,![]() ,即可满足要求.
,即可满足要求.
故当![]() 时,命题成立.
时,命题成立.
其次,证明![]() 时,命题不成立.为此,我们举反例.
时,命题不成立.为此,我们举反例.
取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
于是,对于任意的6个整数![]() ,
,![]() ,
,![]() ,
,
和式![]() 都是3的倍数.
都是3的倍数.
则![]()
![]()
![]()
![]() .
.
不妨设![]() 中不为零且下标
中不为零且下标![]() 为最大的数是
为最大的数是![]() ,即
,即![]() ,且
,且![]() ,则
,则
![]()
![]() .
.
另外,不妨设![]() (当
(当![]() 时,可考虑
时,可考虑![]() .
.
若![]() ,则
,则![]()
![]()
![]()
![]() .
.
若![]() ,则
,则![]() ,
,![]() .
.
综上可知![]() ,且
,且![]() ,
,![]() .
.
显然2003与3互素.
假若有2003整除![]() ,则
,则![]() ,
,![]() 为整数,且
为整数,且![]() .于是,
.于是,![]() ,这与
,这与![]() 矛盾.因此,当取
矛盾.因此,当取![]() ,
,![]() 时,就不可能有
时,就不可能有![]() ,
,![]() ,
,![]() ,
,![]() ,能使得
,能使得
![]() .
.
这个反例说明:当![]() 时,命题不成立.
时,命题不成立.
由上述两步可知,所求的最小正整数![]() 为7.
为7.


科目:高中数学 来源: 题型:
【题目】三台县某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的![]() 天内,西红柿市场售价与上市时间的关系为
天内,西红柿市场售价与上市时间的关系为![]() ;西红柿的种植成本与上市时间的关系为
;西红柿的种植成本与上市时间的关系为![]() .认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?最大收益是多少?(注:市场售价各种植成本的单位:元/
.认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?最大收益是多少?(注:市场售价各种植成本的单位:元/![]() ,时间单位:天)
,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求证:BF∥平面ADE;
(2)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1+ax+by)n的展开式中不含y的项的系数的绝对值的和为32,则a,n的值可能为( )
A.a=2,n=5B.a=1,n=6C.a=-1,n=5D.a=1,n=5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得数据如下表(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(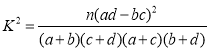 ,其中
,其中 ![]() )
)
抗倒伏数据如下:
143 147 147 151 153 153 157 159 160 164 166 169 174 175 175
180 188 188 192 195 195 199 203 206 206
易倒伏数据如下:
151 167 175 178 181 182 186 186 187 190 190 193 194 195 198
199 199 202 202 203
(1)完成 2×2 列联表,并说明能否在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,再从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,求X的分布列(概率用组合数算式表示);
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的![]() ,都有
,都有![]() ;②对于任意的
;②对于任意的![]() 都有
都有![]() ③函数
③函数![]() 的图象关于y轴对称,则下列结论中正确的是( )
的图象关于y轴对称,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com