练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】三台县某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的天内，西红柿市场售价与上市时间的关系为；西红柿的种植成本与上市时间的关系为.认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？最大收益是多少？（注：市场售价各种植成本的单位：元/，时间单位：天）

    【答案】从二月一日开始的第50天上市时，西红柿的纯收益最大，最大收益为100元/102kg.

    【解析】

    根据题意得出西红柿的纯收益的表达式，利用二次函数的性质得出分段函数每一段的最大值，即可得出结论.

    设时刻上市的西红柿的纯收益为

    则依题意有

    当时，配方整理得

    则当时，取得区间上的最大值为100；

    当时，配方整理得，

    则当时，取得区间上的最大值为87.5.

    综上，当时，在区间上可以取得最大值100

    故从二月一日开始的第50天上市时，西红柿的纯收益最大，最大收益为100元/102kg.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司在过去几年内使用某种型号的灯管1 000根，该公司对这些灯管的使用寿命（单位：h）进行了统计，统计结果如表所示：

    分组

    频数

    48

    121

    208

    223

    频率

    分组

    频数

    193

    165

    42

    频率

    （1）将各组的频率填入表中；

    （2）根据上述统计结果，估计该种型号灯管的使用寿命不足1500 h的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题共13分）

    如图，正方形ABCD和四边形ACEF所在的平面互相垂直。

    EF//AC，AB=,CE=EF=1

    （Ⅰ）求证：AF//平面BDE；

    （Ⅱ）求证：CF⊥平面BDF;

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“开门大吉”是某电视台推出的游戏节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎)，选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金.在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40(单位：岁).其猜对歌曲名称与否的人数如图所示.

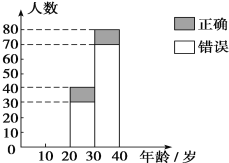
    （1）写出2×2列联表；判断能否在犯错误的概率不超过0.10的前提下认为猜对歌曲名称与年龄有关系，说明你的理由.(下面的临界值表供参考)

    P(K2≥k0)

    0.10

    0.05

    0.010

    0.005

    k0

    2.706

    3.841

    6.635

    7.879

    （2）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，求20～30岁与30～40岁各有几人.

    参考公式：K2＝，其中n＝a＋b＋c＋d.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的实轴长为4，焦距为．

    （1）求椭圆C的标准方程；

    （2）设直线l经过点且与椭圆C交于不同的两点M，N（异于椭圆的左顶点），设点Q是x轴上的一个动点．直线QM，QN的斜率分别为，，试问：是否存在点Q，使得为定值？若存在．求出点Q的坐标及定值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从参加高二年级期末考试的学生中抽出60名学生，并统计了他们的化学成绩（成绩均为整数且满分为100分），把其中不低于50分的分成五段，，…，后画出如图部分频率分布直方图．观察图形的信息，回答下列问题：

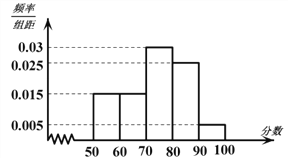
    （1）求出这60名学生中化学成绩低于50分的人数；

    （2）估计高二年级这次考试化学学科及格率（60分以上为及格）；

    （3）从化学成绩不及格的学生中随机调查1人，求他的成绩低于50分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解地区足球特色学校的发展状况，某调查机构得到如下统计数据：

    年份

    2014

    2015

    2016

    2017

    2018

    足球特色学校（百个）

    0.30

    0.60

    1.00

    1.40

    1.70

    （1）根据上表数据，计算与的相关系数，并说明与的线性相关性强弱（已知：，则认为与线性相关性很强；，则认为与线性相关性一般；，则认为与线性相关性较弱）；

    （2）求关于的线性回归方程，并预测地区2019年足球特色学校的个数（精确到个）.

    本题参考公式和数据：，，，，，.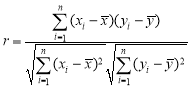

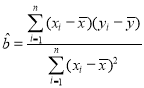    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】试求出正整数的最小可能值，使得下述命题成立：对于任意的个整数（允许相等），必定存在相应的个整数（也允许相等），且，，使得2003能整除.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线（为参数，实数），曲线（为参数，实数）.在以为极点，轴的正半轴为极轴的极坐标系中，射线与交于，两点，与交于，两点.当时，；当，.

    （1）求和的值.

    （2）求的最大值.

    查看答案和解析>>

    同步练习册答案