
| 产品数量x(件) | 6 | 10 | 20 |
| 成本合计y(元) | 1040 | 1600 | 3700 |
分析 (1)把表格中的数据对代入二次函数解析式,求解a,b,c的值,则成本函数可求;
(2)由收入减去成本得到利润函数p=p(x);
(3)直接求解利润函数对应的方程,得到函数的两个零点,由此可以得到盈利和亏损时的产品数量的范围.
解答 解:(1)将表格中相关数据代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{36a+6b+c=1040}\\{100a+10b+c=1600}\\{400a+20b+c=3700}\end{array}\right.$,
解得a=5,b=60,c=500.
∴y=f(x)=5x2+60x+500,(x≥0);
(2)∵x(百件)在每件销售价为200元时的收入为200(百元)=20(千元),
∴p=p(x)
=20x-f(x)
=20x-(5x2+60x+500)
=-5x2-40x+500,(x≥0);
(3)令p(x)=0,即-5x2-40x+500=0,
解得x=-4-2$\sqrt{58}$(舍)或x=-4+2$\sqrt{58}$≈11.23,
故0<x<11.23时,p(x)>0;x>11.23时,p(x)<0,
∴当产品数量为1123件时由盈变亏.
点评 本题考查了函数模型的选择及应用,考查了简单的数学建模思想方法,解答此题的关键是注意单位的统一,是中档题,也是易错题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
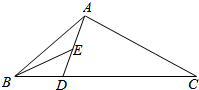 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{4\sqrt{2}}{3}$)∪($\frac{4\sqrt{2}}{3}$,+∞) | B. | [-$\frac{4\sqrt{2}}{3}$,0] | C. | (-∞,-3$\sqrt{2}$]∪[3$\sqrt{2}$,+∞) | D. | [0,$\frac{4\sqrt{2}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com