
(本小题满分12分)
在一次数学考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.某考生有5道题已选对正确答案,其余题中有两道只能分别判断2个选项是错误的,还有1道题因不理解题意只好乱猜.
(1) 求该考生8道题全答对的概率;
(2)若评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”,求该考生所得分数的分布列.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量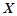 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)电信公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为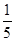 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
(I)求X的分布列;(II)试说明小李出资50元增加1张奖券是否划算。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病.经调查发现一家工厂排出的废水中含有甲基汞,使鱼类受到污染.人们长期食用含高浓度甲基汞的鱼类引起汞中毒. 引起世人对食品安全的关注.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm.
罗非鱼是体型较大,生命周期长的食肉鱼,其体内汞含量比其他鱼偏高.现从一批罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如下:
(Ⅰ)若某检查人员从这15条鱼中,随机地抽出3条,求恰有1条鱼汞含量超标的概率;
(Ⅱ)以此15条鱼的样本数据来估计这批鱼的总体数据.若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的鱼汞含量超标的条数,求ξ的分布列及Eξ
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
公安部发布酒后驾驶处罚的新规定(一次性扣罚12分)已于2011年4月1日起正式施行.酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量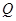 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当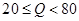 时,为酒后驾车;当
时,为酒后驾车;当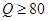 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(Ⅰ)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(Ⅱ)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率. (酒后驾车的人用大写字母如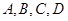 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如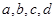 表示)
表示)
| 血酒含量 | (0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com