
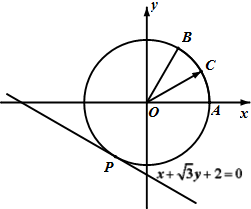
 ČçÍźŁŹÔ˛OÓëÖąĎßx+
ČçÍźŁŹÔ˛OÓëÖąĎßx+| 3 |
| 3 |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
|
| 2 | ||||
|
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
2
| ||
| 3 |
2
| ||
| 3 |
|
|
|
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 17 |
| 9 |
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 2 |
| ||
| 3 |
| |OA1|2-|OB1|2 |
2
| ||
| 3 |
| ||
|
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |


 ĚěĚěĎňÉĎŇťąžşĂžíĎľÁĐ´đ°¸
ĚěĚěĎňÉĎŇťąžşĂžíĎľÁĐ´đ°¸ ХѧÉú10ˇÖÖÓÓŚÓĂĚâĎľÁĐ´đ°¸
ХѧÉú10ˇÖÖÓÓŚÓĂĚâĎľÁĐ´đ°¸
| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 5 |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| AĄ˘{x|xŁź1} |
| BĄ˘{x|xŁž1} |
| CĄ˘{x|0ŁźxŁź1} |
| DĄ˘∅ |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| AĄ˘Ł¨1ŁŹ2ŁŠ |
| BĄ˘Ł¨2ŁŹ+ĄŢŁŠ |
| CĄ˘Ł¨1ŁŹ2] |
| DĄ˘[2ŁŹ+ĄŢŁŠ |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
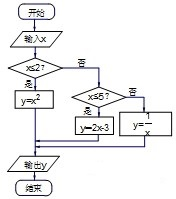
| AĄ˘1 | BĄ˘2 | CĄ˘3 | DĄ˘4 |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
 ČçÍźŁŹŇŃÖŞÖąĎßl1Łşy=4x+mŁŹŁ¨mŁź0ŁŠÓëĹ×ÎďĎßC1Łşy=2ax2ŁŹ(aŁž0)şÍÔ˛C2Łşx2+(y+1)2=17śźĎŕÇĐŁŹFĘÇĹ×ÎďĎßC1ľÄ˝šľăŁŽ
ČçÍźŁŹŇŃÖŞÖąĎßl1Łşy=4x+mŁŹŁ¨mŁź0ŁŠÓëĹ×ÎďĎßC1Łşy=2ax2ŁŹ(aŁž0)şÍÔ˛C2Łşx2+(y+1)2=17śźĎŕÇĐŁŹFĘÇĹ×ÎďĎßC1ľÄ˝šľăŁŽ˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| x 2 |
| 8 |
| y 2 |
| 4 |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
˛éż´´đ°¸şÍ˝âÎö>>
šúźĘѧУÓĹŃĄ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com