
| x 2 |
| 8 |
| y 2 |
| 4 |
| x12 |
| 8 |
| y12 |
| 4 |
| x22 |
| 8 |
| y22 |
| 4 |
| 4(x2-x1) |
| 8 |
| -2(y2-y1) |
| 4 |
| y2-y1 |
| x2-x1 |
| 10 |
| 3 |
| 1+k2 |
4
| ||
| 3 |
| 5 | ||
|
5
| ||
| 2 |
| 1 |
| 2 |
5
| ||
| 3 |


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
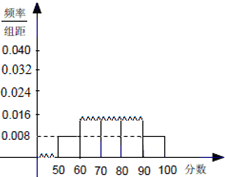 随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.查看答案和解析>>
科目:高中数学 来源: 题型:
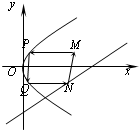 如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )
如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )| A、5 | B、6 | C、7 | D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
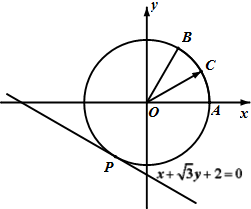 如图,圆O与直线x+
如图,圆O与直线x+| 3 |
| 3 |
| OC |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| 1 |
| |MN| |
| 1 |
| |PQ| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| x2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com