
| A. | |a|=4 | B. | a=-4且b2+16c>0 | C. | a<0且b2+4ac≤0 | D. | 以上说法都不对 |
分析 设y=ax2+bx+c与x轴相交于两点(x1,0),(x2,0),a<0.可得|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{\sqrt{{b}^{2}-4ac}}{-a}$.由题意可得:$\left\{\begin{array}{l}{a<0}\\{△={b}^{2}-4ac>0}\\{|{x}_{1}-{x}_{2}|=\sqrt{\frac{4ac-{b}^{2}}{4a}}}\end{array}\right.$,化简即可得出.
解答 解:设y=ax2+bx+c与x轴相交于两点(x1,0),(x2,0),a<0.
则${x}_{1}+{x}_{2}=-\frac{b}{a}$,x1x2=$\frac{c}{a}$.
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(-\frac{b}{a})^{2}-\frac{4c}{a}}$=$\frac{\sqrt{{b}^{2}-4ac}}{-a}$.
由题意可得:$\left\{\begin{array}{l}{a<0}\\{△={b}^{2}-4ac>0}\\{|{x}_{1}-{x}_{2}|=\sqrt{\frac{4ac-{b}^{2}}{4a}}}\end{array}\right.$,
由$\sqrt{\frac{4ac-{b}^{2}}{4a}}$=$\frac{\sqrt{{b}^{2}-4ac}}{-a}$,解得a=-4.
∴实数a,b,c满足a=-4,△=b2+16c>0,
故选:B.
点评 本题考查了二次函数的性质、一元二次方程的实数根与判别式的关系及其根与系数的关系,考查了推理能力与计算能力,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |
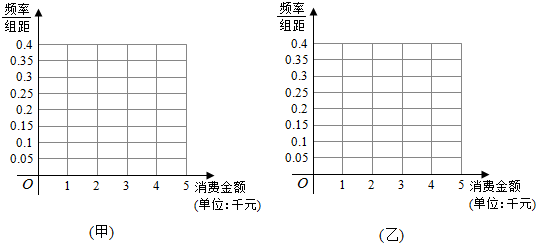
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{7}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
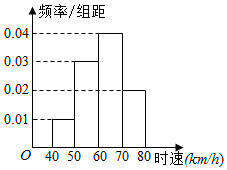 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | ||
| C. | 3 | D. | 条件不足,无法计算 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{43}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\sqrt{73}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com