
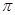 为圆周率,
为圆周率,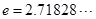 为自然对数的底数.
为自然对数的底数.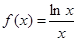 的单调区间;
的单调区间;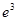 ,
,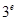 ,
,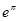 ,
,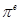 ,
,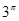 ,
,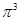 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;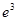 ,
,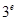 ,
,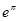 ,
,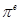 ,
,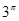 ,
,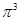 这6个数按从小到大的顺序排列,并证明你的结论.
这6个数按从小到大的顺序排列,并证明你的结论.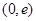 ,单调减区间为
,单调减区间为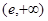 ;(2)最大数为
;(2)最大数为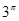 ,最小数为
,最小数为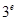 ;(3)
;(3)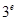 ,
,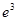 ,
,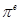 ,
,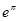 ,
,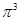 ,
,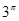 .
.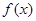 的定义域,用导数法求函数
的定义域,用导数法求函数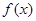 的单调区间;(2)利用(1)的结论结合函数根据函数
的单调区间;(2)利用(1)的结论结合函数根据函数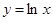 、
、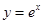 、
、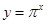 的性质,确定
的性质,确定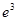 ,
,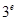 ,
,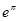 ,
,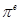 ,
,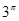 ,
,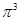 这6个数中的最大数与最小数;(3)由(1),(2)的结论只需比较
这6个数中的最大数与最小数;(3)由(1),(2)的结论只需比较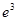 与
与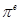 和
和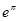 与
与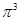 的大小,
的大小,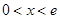 时,
时,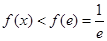 ,即
,即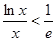 ,在上式中,令
,在上式中,令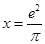 ,又
,又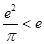 ,则
,则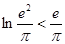 ,即得
,即得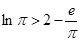 ,整理得
,整理得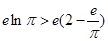 ,估算
,估算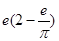 的值,比较
的值,比较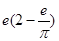 与3的大小,从而确定
与3的大小,从而确定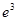 与
与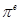 的大小关系,再根据
的大小关系,再根据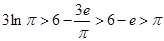 ,确定
,确定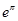 与
与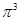 的大小关系,最后确定6个数从小到大的顺序.
的大小关系,最后确定6个数从小到大的顺序.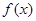 的定义域为
的定义域为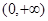 ,因为
,因为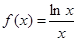 ,所以
,所以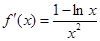 ,
,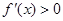 ,即
,即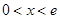 时,函数
时,函数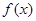 单调递增;
单调递增;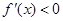 ,即
,即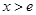 时,函数
时,函数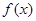 单调递减;
单调递减;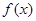 的单调增区间为
的单调增区间为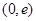 ,单调减区间为
,单调减区间为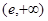 .
.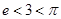 ,所以
,所以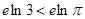 ,
,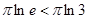 ,即
,即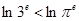 ,
,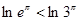 ,
,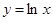 、
、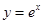 、
、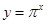 在定义域上单调递增,
在定义域上单调递增,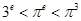 ,
,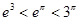 ,
,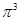 与
与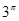 之中,最小数在
之中,最小数在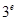 与
与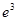 之中,
之中,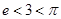 及(1)的结论得
及(1)的结论得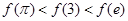 ,即
,即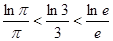 ,
,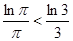 得
得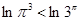 ,所以
,所以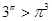 ,
,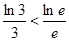 得
得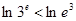 ,所以
,所以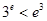 ,
,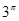 ,最小数为
,最小数为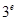 .
.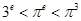 ,
,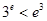 ,又由(2)知,
,又由(2)知,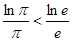 ,
,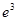 与
与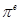 和
和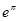 与
与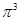 的大小,
的大小,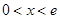 时,
时,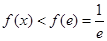 ,即
,即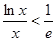 ,
,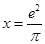 ,又
,又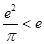 ,则
,则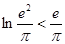 ,即得
,即得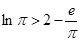 ①
①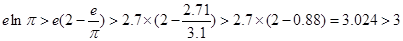 ,
,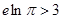 ,亦即
,亦即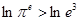 ,所以
,所以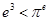 ,
,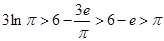 ,即
,即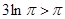 ,所以
,所以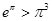 ,
,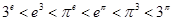 ,即6个数从小到大的顺序为
,即6个数从小到大的顺序为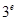 ,
,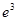 ,
,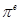 ,
,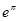 ,
,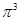 ,
,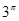 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com