
 ,设
,设 为
为 的导数,
的导数,
 的值;
的值; ,等式
,等式 都成立.
都成立. 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:不详 题型:解答题
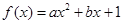 (
(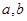 为实数,
为实数,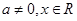 ),
),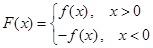 ,⑴若
,⑴若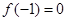 ,且函数
,且函数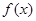 的值域为
的值域为 ,求
,求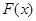 的表达式;
的表达式;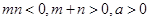 ,且函数
,且函数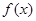 为偶函数,判断
为偶函数,判断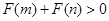 是否大0?
是否大0?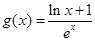 ,当
,当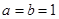 时,证明:对任意实数
时,证明:对任意实数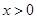 ,
,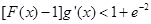 (其中
(其中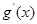 是
是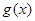 的导函数) .
的导函数) .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
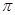 为圆周率,
为圆周率,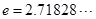 为自然对数的底数.
为自然对数的底数.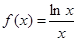 的单调区间;
的单调区间;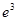 ,
,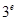 ,
,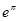 ,
,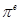 ,
,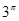 ,
,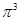 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;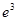 ,
,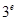 ,
,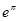 ,
,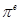 ,
,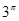 ,
,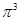 这6个数按从小到大的顺序排列,并证明你的结论.
这6个数按从小到大的顺序排列,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
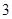 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交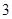 元的管理费,预计当每件产品的售价为
元的管理费,预计当每件产品的售价为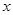 元(
元(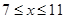 )时,一年的销售量为
)时,一年的销售量为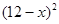 万件.
万件.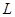 (万元)与每件产品的售价
(万元)与每件产品的售价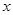 的函数关系式;
的函数关系式;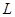 最大?并求出
最大?并求出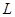 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com