
分析 (1)求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(2)问题转化为a<2x2-x在(1,+∞)恒成立,结合二次函数的性质求出a的范围即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{a}{x}$-4x=$\frac{a-{4x}^{2}}{x}$,
令f′(x)>0,解得:x<$\frac{\sqrt{a}}{2}$,
令f′(x)<0,解得:x>$\frac{\sqrt{a}}{2}$,
∴f(x)在(0,$\frac{\sqrt{a}}{2}$)递增,在($\frac{\sqrt{a}}{2}$,+∞)递减;
(2)若对任意x1,x2∈(1,+∞),x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<-1,
即若对任意x1,x2∈(1,+∞),x1≠x2,都有f′(x)=$\frac{a}{x}$-2x<-1,
∴a<2x2-x在(1,+∞)恒成立,
令g(x)=2x2-x=2${(x-\frac{1}{4})}^{2}$-$\frac{1}{8}$,
∴g(x)min=g(1)=1,
∴a<1.
点评 本题考察了导数的应用,考察函数的单调性问题,考察函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
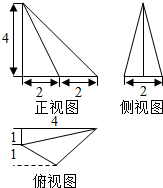
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
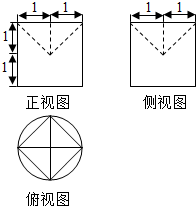
| A. | 2π-$\frac{2}{3}$ | B. | 2π-$\frac{4}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
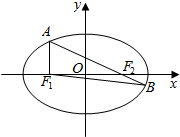 如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.
如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com