
分析 由条件可设直线l的方程为y=x+b,带入椭圆方程便可得到5x2+2bx+b2-4=0,可设M(x1,y1),N(x2,y2),从而有${x}_{1}+{x}_{2}=-\frac{2b}{5},{x}_{1}{x}_{2}=\frac{{b}^{2}-4}{5}$,根据弦长公式便可得到$|MN|=\frac{4\sqrt{2}}{5}•\sqrt{5-{b}^{2}}=2$,解出b值,从而便可得出直线l的方程.
解答 解:根据条件设l的方程为:y=x+b,带入椭圆的方程并整理得:
5x2+2bx+b2-4=0;
设M(x1,y1),N(x2,y2),则:${x}_{1}+{x}_{2}=-\frac{2b}{5},{x}_{1}{x}_{2}=\frac{{b}^{2}-4}{5}$;
∴$|MN|=\sqrt{2}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}•\sqrt{\frac{4{b}^{2}}{25}-\frac{4({b}^{2}-4)}{5}}$=$\frac{4\sqrt{2}}{5}•\sqrt{5-{b}^{2}}=2$;
∴解得$b=±\frac{\sqrt{30}}{4}$;
∴直线l的方程为$y=x+\frac{\sqrt{30}}{4}$,或$y=x-\frac{\sqrt{30}}{4}$.
点评 考查直线垂直时斜率的关系,直线的斜截式方程,椭圆的标准方程,以及韦达定理,弦长公式.


科目:高中数学 来源: 题型:填空题
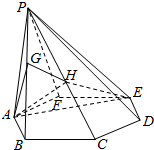 底面为正六边形的六棱锥P-ABCDE,$\overrightarrow{PG}$=$\frac{1}{2}$$\overrightarrow{GB}$,$\overrightarrow{PH}$=$\overrightarrow{HC}$,记三棱锥G-PAH的体积为V1,三棱锥H-PAE的体积为V2,则V1:V2是$\frac{1}{9}$.
底面为正六边形的六棱锥P-ABCDE,$\overrightarrow{PG}$=$\frac{1}{2}$$\overrightarrow{GB}$,$\overrightarrow{PH}$=$\overrightarrow{HC}$,记三棱锥G-PAH的体积为V1,三棱锥H-PAE的体积为V2,则V1:V2是$\frac{1}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
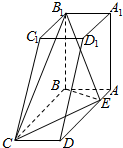 如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.
如图所示的几何体A1B1C1D1-ABCD中,平面A1B1C1D1∥平面ABCD,A1B1C1D1是边长为2的正方形,ABCD是矩形,AD=5,AA1B1B是矩形,A1A⊥平面ABCD,E为AD上的一点,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
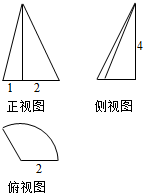
| A. | $\frac{2π}{3}$ | B. | $\frac{16π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com