
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用等差数列与等比数列的前n项和公式即可得出.
解答 解:(1)设数列{an}的公比为q(q>0),由a2+a3=24得:2q+2q2=24,
解得:q=3或q=-4(舍去),
∴${a_n}=2•{3^{n-1}}$,
设数列{bn}的公差为d(d≠0),由已知,$\left\{\begin{array}{l}{({b_1}+d)^2}={b_1}({b_1}+4d)\\ 3{b_1}+5d=13\end{array}\right.$,
解得:d=0(舍去)或d=2,这时b1=1,
∴bn=2n-1,
(2):设数列{an}的前n项和为Tn,则${T_n}=\frac{{2(1-{3^n})}}{1-3}={3^n}-1$,
设数列{bn}的前n项和为Ln,则${L_n}=\frac{n(1+2n-1)}{2}={n^2}$,
∴${S_n}={T_n}-{L_n}={3^n}-{n^2}-1$.
另解:Sn=(a1+a2+…+an)-(b1+b2+…+bn)=$\frac{{2(1-{3^n})}}{1-3}-\frac{n(1+2n-1)}{2}={3^n}-{n^2}-1$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
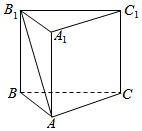 如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.
如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x-π)一定是奇函数 | B. | f(x-π)一定是偶函数 | ||
| C. | f(x+π)一定是奇函数 | D. | f(x+π)一定是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{2}}{2}$,1] | B. | [$\frac{\sqrt{3}}{3}$,1] | C. | [$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{5}}{5}$] | D. | [$\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{5}}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com