
分析 (1)根据直线和圆相交,利用弦长公式进行求解即可.
(2)利用直线和圆相切的条件,建立方程关系进行求解判断.
解答 解:(1)圆C的方程可化为(x-3)2+(y-4)2=25+5t
故圆心为C(3,4),半径$r=\sqrt{25+5t}$
则圆心C到直线l的距离为$d=\frac{|3+12+15|}{{\sqrt{{1^2}+{3^2}}}}=3\sqrt{10}$
又弦长为$2\sqrt{10}$,则$r=\sqrt{{{(3\sqrt{10})}^2}+{{(\sqrt{10})}^2}}=10$即$\sqrt{25+5t}=10$,解得t=15…(4分)
(2)当t=1时,圆C的方程为x2+y2-6x-8y-5=0①
则圆心为C(3,4),半径$r=\sqrt{30}<3\sqrt{10}$,圆C与直线l相离假设在直线AB上存在一个定点满足条件,设动点P(m,n)
由已知得PA⊥AC,PB⊥BC
则A,B在以CP为直径的圆(x-3)(x-m)+(y-4)(y-n)=0
即x2+y2-(3+m)x-(4+n)y+3m+4n=0上②…(7分)
①-②得,直线AB的方程为(m-3)x+(n-4)y-3m-4n-5=0③
又点P(m,n)在直线l上,则m+3n+15=0,即m=-3n-15,代入③式
得(-3n-18)x+(n-4)y+9n+45-4n-5=0
即直线AB的方程为18x+4y-40+n(3x-y-5)=0…(10分)
因为上式对任意n都成立,故$\left\{\begin{array}{l}3x-y-5=0\\ 18x+4y-40=0\end{array}\right.$,得$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$
故在直线AB上存在一个定点,定点坐标为(2,1)…(12分)
点评 本题主要考查直线和圆相交的弦长的计算和应用,利用直线和圆的位置关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
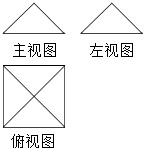 一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{6}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
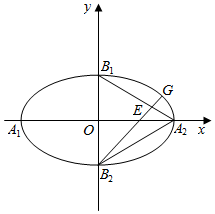 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 4π | C. | 9π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
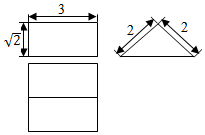
| A. | $\frac{17\sqrt{17}}{6}$π | B. | 34π | C. | 17π | D. | $\frac{17}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com