对于三次函数f(x)=ax3+bx2+cx+d(a≠0).
定义:(1)设f''(x)是函数y=f(x)的导数y=f'(x)的导数,若方程f''(x)=0有实数解x,则称点(x,f(x))为函数y=f(x)的“拐点”;
定义:(2)设x为常数,若定义在R上的函数y=f(x)对于定义域内的一切实数x,都有f(x+x)+f(x-x)=2f(x)成立,则函数y=f(x)的图象关于点(x,f(x))对称.
已知f(x)=x3-3x2+2x+2,请回答下列问题:
(1)求函数f(x)的“拐点”A的坐标
(2)检验函数f(x)的图象是否关于“拐点”A对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数G(x),使得它的“拐点”是(-1,3)(不要过程)
【答案】
分析:(1)根据“拐点”的定义求出f''(x)=0的根,然后代入函数解析式可求出“拐点”A的坐标.
(2)由(1)知“拐点”坐标是(1,2),然后计算f(1+x)+f(1-x)可得等于2f(1),根据定义(2)可得结论,一般地,三次函数f(x)=ax
3+bx
2+cx+d(a≠0)的“拐点”是
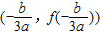
,它就是f(x)的对称中心.
(3)根据“拐点”的定义可写出符合条件的三次函数.
解答:解:(1)依题意,得:f'(x)=3x
2-6x+2,∴f''(x)=6x-6.…(2分)
由f''(x)=0,即6x-6=0.∴x=1,又 f(1)=2,
∴f(x)=x
3-3x
2+2x+2的“拐点”坐标是(1,2).…(4分)
(2)由(1)知“拐点”坐标是(1,2).
f(1+x)+f(1-x)=(1+x)
3-3(1+x)
2+2(1+x)+2+(1-x)
3-3(1-x)
2+2(1-x)+2=2+6x
2-6-6x
2+4+4=4=2f(1),
由定义(2)知:f(x)=x
3-3x
2+2x+2关于点(1,2)对称.…(8分)
一般地,三次函数f(x)=ax
3+bx
2+cx+d(a≠0)的“拐点”是
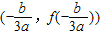
,它就是f(x)的对称中心.…(10分)
(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数…)都可以给分
(3)G(x)=a(x+1)
3+b(x+1)+3(a≠0)或写出一个具体的函数,
如G(x)=x
3+3x
2+3x+4或G(x)=x
3+3x
2-x.…(12分)
点评:本题在函数、导数、方程的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放性,情景新颖,解题的关键是:深刻理解函数“拐点”的定义和函数图象的对称中心的意义.其本质是:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;且任何一个三次函数的拐点就是它的对称中心,即
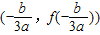
.

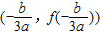 ,它就是f(x)的对称中心.
,它就是f(x)的对称中心.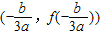 ,它就是f(x)的对称中心.…(10分)
,它就是f(x)的对称中心.…(10分)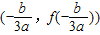 .
. 
