
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,如果方程
时,如果方程![]() 有两个不等实根
有两个不等实根![]()
![]() ,求实数t的取值范围,并证明
,求实数t的取值范围,并证明![]() .
.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;当
;当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)求出![]() ,对
,对![]() 分类讨论,分别求出
分类讨论,分别求出![]() 的解,即可得出结论;
的解,即可得出结论;
(2)由(1)得出![]() 有两解时
有两解时![]() 的范围,以及
的范围,以及![]() 关系,将
关系,将![]() ,等价转化为证明
,等价转化为证明![]() ,不妨设
,不妨设![]() ,令
,令![]() ,则
,则![]()
![]() ,即证
,即证![]() ,构造函数
,构造函数![]() ,只要证明对于任意
,只要证明对于任意![]() 恒成立即可.
恒成立即可.
(1)![]() 的定义域为R,且
的定义域为R,且![]() .
.
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
故当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
单调递减区间是![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
单调递减区间是![]() .
.
(2)由(1)知当![]() 时,
时,![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,直线
时,直线![]() 与
与![]() 的图像有两个交点,
的图像有两个交点,
![]() 实数t的取值范围是
实数t的取值范围是![]() .
.
![]() 方程
方程![]() 有两个不等实根
有两个不等实根![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
要证![]() ,只需证
,只需证![]() ,
,
即证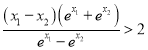 ,不妨设
,不妨设![]() .
.
令![]() ,则
,则![]()
![]() ,
,
则要证![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() 成立,
成立,
即![]() 成立.
成立.![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求实数a的值;
,求实数a的值;
(2)若函数![]() 有2个不同的零点
有2个不同的零点![]() ,
,![]() .
.
①求实数a的取值范围;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生M的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
推出的多款健康运动软件中的一款,大学生M的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、
、![]() 步,(说明:“
步,(说明:“![]() ”表示大于或等于0,小于2000,以下同理),
”表示大于或等于0,小于2000,以下同理),![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,且
步,且![]() 、
、![]() 、
、![]() 三种类别的人数比例为
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
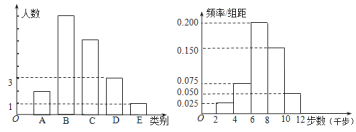
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在![]() 的人数;
的人数;
(Ⅱ)若在大学生![]() 该天抽取的步数在
该天抽取的步数在![]() 的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.
的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,点E,F分别为AD,BP的中点,AD=3,AP=3![]() ,PC
,PC![]() .
.
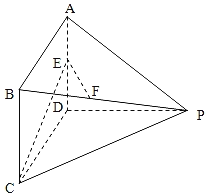
(1)求证:EF//平面PDC;
(2)若∠CDP=120°,求二面角E﹣CP﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.
(1)证明:![]() ;
;
(2)是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com